
题目列表(包括答案和解析)
数的y随x增大而增大,且点P(b,k)与Q(1,-![]() )关于原点对称,则适合题意
)关于原点对称,则适合题意
的k、b的值为k=________,b=________。
观察可得最简公分母是(x+1)(x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【解答】
(2)方程的两边同乘(x+1)(x-1),得
2(x-1)+4=x2-1,
即x2-2x-3=0,
(x-3)(x+1)=0,
解得x1=3,x2=-1,
检验:把x=3代入(x+1)(x-1)=8≠0,即x=3是原分式方程的解,
把x=-1代入(x+1)(x-1)=0,即x=-1不是原分式方程的解,
则原方程的解为:x=3.
【点评】此题考查了![]() 实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
20.(本题满分5分)如图,已知△ABC,且∠ACB=90°。
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明);
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
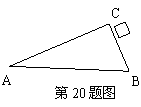 |
阅读理解:对于任意正实数a、b,∵ ≥0,∴
≥0,∴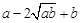 ≥0,
≥0,
∴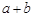 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在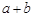 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为 ,考虑何时时周长
,考虑何时时周长 最小。
最小。
∵m>0,  (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m= 时,镜框周长 有最小值是 ;
有最小值是 ;
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.

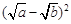 ≥0,∴
≥0,∴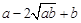 ≥0,
≥0,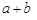 ≥
≥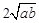 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.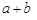 ≥
≥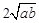 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥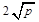 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值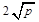 .
.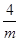 ,考虑何时时周长
,考虑何时时周长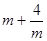 最小。
最小。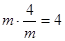 (定值),由以上结论可得:
(定值),由以上结论可得: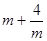 有最小值是 ;
有最小值是 ;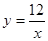 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.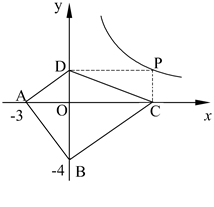
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com