
题目列表(包括答案和解析)
由方程组 可得出x与y的关系是( )
可得出x与y的关系是( )
A、x+y=1 B、x+y=﹣1
C、x+y=7 D、x+y=﹣7
【解析】先把方程组化为 的形式,再把两式相加即可得到关于x、y的关系式.
的形式,再把两式相加即可得到关于x、y的关系式.
由方程组 可得出x与y的关系是( )
可得出x与y的关系是( )
A、x+y=1 B、x+y=﹣1
C、x+y=7 D、x+y=﹣7
【解析】先把方程组化为 的形式,再把两式相加即可得到关于x、y的关系式.
的形式,再把两式相加即可得到关于x、y的关系式.
李丽同学参加七年级地理兴趣小组,打算做一个地球和太阳的模型,以展示太阳与地球之间的关系.大家都知道,太阳比地球大,可是大多少呢?如何寻找制作模型的依据呢?李丽制定了一个方案:
第一步:她认为地球和太阳都可以近似地看作是球体,由球体的体积公式V=![]() πR3(R是半径),只需要知道地球和太阳的半径之间的关系,就能确定模型球体的大小了.
πR3(R是半径),只需要知道地球和太阳的半径之间的关系,就能确定模型球体的大小了.
第二步:她查找天文资料可以找到地球的直径约为1.28×104km,太阳的直径约为1.4×106km.
第三步:李丽开始动手制作地球模型,取地球半径为4cm.
第四步:李丽依照算得的数据制作出了相应的太阳模型.
李丽的方案正确吗?你认为她的做法有道理吗?在这些过程中,李丽必须计算出哪些量?
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
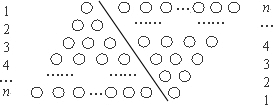
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com