
题目列表(包括答案和解析)
计算:
 ;
;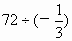 ;
; .
.计算:
(1)2.9×(-0.4); (2)-30.5×0.2; (3)100×(-0.001);
(4)-4.8×(-1.25); (5)-7.6×0.03; (6)-4.5×(-0.32);
同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道![]() 时,我们可以这样做:
时,我们可以这样做:
(1)观察并猜想:
12+22=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
12+22+32=(1+0)×1+(1+1)×2+(l+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
12+22+32+42=(1+0)×1+(1+1)×2+(l+2)×3+(1+3)×4;
=1+0×1+2+1×2+3+2×3+________
=(1+2+3+4)+________
(2)归纳结论:
12+22+32…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…[(1+(n-l)]n
=1+0×1+2+1×2+3+2×3+…+n+(n-1)×n
=________+________
=________+________
=![]() ×________
×________
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com