
题目列表(包括答案和解析)
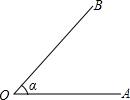 如图,我们可将这个角表示为
如图,我们可将这个角表示为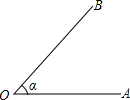 如图,我们可将这个角表示为________或________或________,另外我们还可以用________来表示角.
如图,我们可将这个角表示为________或________或________,另外我们还可以用________来表示角.
| 1 |
| 2 |
 |
| LN |
 |
| LN |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
 |
| RT |
 |
| PQ |
 |
| RT |
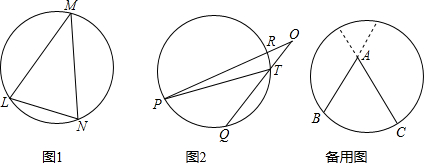
 种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
种不同于(3)的正确证明吗?我们将对你的出色表现另外奖励3分.
| y=x2+px+q | p | q | △ | x1 | x2 | d | ||||||||
| y=x2-5x+6 | -5 | 6 | 1 | 2 | 3 | 1 | ||||||||
y=x2-
|
-
|
|
|
|||||||||||
| y=x2+x-2 | -2 | -2 | 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com