
题目列表(包括答案和解析)
| 某县种植了一种无公害蔬菜,为了扩大生产规模,该县决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元,随着补贴数额的不断增大,生产规模也不断增加,但每亩蔬菜的收益会相应降低,经调查,种植亩数y(亩)、每亩蔬菜的收益z(元)与补贴数额x(元)之间的关系如下表: | ||||||||||||||||||
(3)在取得最大收益的情况下,为了满足市场需求,用不超过70亩的土地对这种蔬菜进行反季节的种植,为此需修建一些蔬菜大棚,修建大棚要用的支架、塑料膜等材料平均每亩的费用为650元,此外还要购置喷灌设备,这项费用(元)与大棚面积(亩)的平方成正比例,比例系数为25,这样,修建大棚后的这部分土地每亩的平均收益比没修前增加了2000元,在扣除修建费后总共增加了85000元.,求修建了多少亩蔬菜大棚?(结果精确到个位,参考数据: 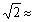 1.414) 1.414) |
如图,已知抛物线y = ax2 + bx-4与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为 .
.
(1)求m的值及抛物线的解析式;
(2)点P是线段 上的一个动点,过点P作PN∥
上的一个动点,过点P作PN∥ ,交
,交 于点
于点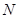 ,连接CP,当
,连接CP,当 的面积最大时,求点P的坐标;
的面积最大时,求点P的坐标;
(3)点 在(1)中抛物线上,点
在(1)中抛物线上,点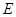 为抛物线上一动点,在
为抛物线上一动点,在 轴上是否存在点
轴上是否存在点 ,使以
,使以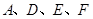 为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com