练习册

  • 练习册
  • 试题
    解:(1)∵∠ACB=∠1+∠2 ∴∠1=∠ACB - ∠2 =90°- 30° =60° (2) ∵CD是△ABC的高 ∴∠ADC= ∵∠ADC=∠1+∠B ∴∠B=∠ADC - ∠1 =90°-30° =60° (3)∵∠ADC+∠2+∠A=180° ∴∠A=180°- ∠ADC - ∠2 =180°- 90°-60° =30° 【查看更多】

     

    题目列表(包括答案和解析)

    （1）已知：如图1，△ABC为正三角形，点M、N分别在BC、CA边上，且BM=CN，BN与AM相交于Q点，试求∠BQM的度数．
    解：∵△ABC为正三角形，∴∠ABC=∠ACB=60°，AB=BC．
    在△ABM和△BCN中，
          
    .
    =
          
    .
    ∠
          
    .
    =∠
          
    .
          
    .
    =
          
    .
    ?△ABM≌△BCN（
     
    ）．
    ∴∠
     
    =∠
     
    ，
    ∴∠BQM=∠
     
    +∠
     
    =∠
     
    +∠
     
    =
     
    °．
    （2）如果将（1）中的正三角形改为正方形ABCD（如图2），点M、N分别在BC、CD边上，且BM=CN，BN与AM相交于Q点，那么∠BQM等于多少度呢？说明理由．
    精英家教网
    （3）如果将（1）中的“正三角形”改为正五边形、正六边形、…、正n边形（如图3），其余条件都不变，请你根据（1）（2）的求解思路，将你推断的结论填入下表：（正多边形的各个内角都相等）
    正多边形 正五边形 正六边形 … 正n边形
    ∠BQM的度数 …
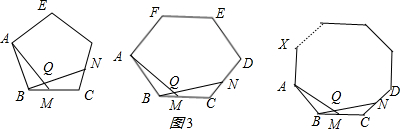
    精英家教网

    查看答案和解析>>

    阅读并填空：
    如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D．请说明△ADC≌△CEB的理由．
    解：∵BE⊥CE于点E（已知），
    ∴∠E=90°
    （垂直的意义）
    （垂直的意义）
    ，
    同理∠ADC=90°，
    ∴∠E=∠ADC（等量代换）．
    在△ADC中，
    ∵∠1+∠2+∠ADC=180°
    （三角形的内角和等于180°）
    （三角形的内角和等于180°）
    ，
    ∴∠1+∠2=90°
    （等式的性质）
    （等式的性质）
    ．
    ∵∠ACB=90°（已知），
    ∴∠3+∠2=90°，
    ∴
    ∠1=∠3（同角的余角相等）
    ∠1=∠3（同角的余角相等）
    ．
    在△ADC和△CEB中，.
    ∠ADC=∠E
    __________
    AC=CB

    ∴△ADC≌△CEB （A．A．S）

    查看答案和解析>>

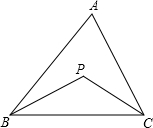    如图BP、CP分别平分∠ABC、∠ACB，请你探索∠A和∠P的数量关系．
    解：∵BP平分∠ABC（已知）
    ∴∠PBC=
    1
    2
    ∠ABC （
    角平分线的定义
    角平分线的定义
    ）．
    同理可得∠PCB=
    1
    2
    ∠ACB
    ∵∠BPC+∠PBC+∠PCB=180°（
    三角形的内角和等于180°
    三角形的内角和等于180°
    ）
    ∴∠BPC=180°-∠PBC-∠PCB （等式的性质）
    =180°-
    1
    2
    （∠ABC+∠ACB ） （
    等量代换
    等量代换
    ）
    =180°-
    1
    2
    （180°-∠
    A
    A
    ）
    =90°+
    1
    2
    ∠
    A
    A
    ．

    查看答案和解析>>

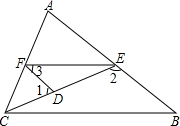    如图，已知∠1+∠2=180°，∠3=∠B，且∠AFE=50°，求∠ACB的度数．
    解：∵∠1+∠2=180° （
    已知
    已知
    ）
    ∠1+∠EDF=180°  （
    邻补角的定义
    邻补角的定义
    ）
    ∴
    ∠2
    ∠2
    =
    ∠EDF
    ∠EDF
     （
    等量代换
    等量代换
    ）
    ∴DF∥
    AB
    AB
     （
    内错角相等，两直线平行
    内错角相等，两直线平行
    ）
    ∴∠3=
    ∠AEF
    ∠AEF
     （
    两直线平行，内错角相等
    两直线平行，内错角相等
    ）
    ∵∠3=∠B
    B
    B
     （
    已知
    已知
    ）
    ∴
    ∠AEF
    ∠AEF
    =
    ∠B
    ∠B
     （
    等量代换
    等量代换
    ）
    ∴
    EF
    EF
    ∥
    BC
    BC
     （
    同位角相等，两直线平行
    同位角相等，两直线平行
    ）
    ∴∠AFE=
    ∠ACB
    ∠ACB
     （
    两直线平行，同位角相等
    两直线平行，同位角相等
    ）
    ∵∠AFE=50° （
    已知
    已知
    ）
    ∴∠ACB=
    50°
    50°
    °．

    查看答案和解析>>

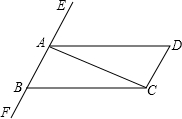    如图，要使AD∥BC，则需添加一个条件，请写出三种情况，并写出简单的推理过程和理由
    解：
    （1）由
    ∠EAD=∠ABC
    ∠EAD=∠ABC
    （填条件）
    得AD∥BC（
    同位角相等，两直线平行
    同位角相等，两直线平行
     ）
    （2）
    由∠DAC=∠ACB，
    得AD∥BC（内错角相等，两直线平行）
    由∠DAC=∠ACB，
    得AD∥BC（内错角相等，两直线平行）
    ；
    （3）
    由∠DAB+∠ABC=180°，
    得AD∥BC（同旁内角互补，两直线平行）．
    由∠DAB+∠ABC=180°，
    得AD∥BC（同旁内角互补，两直线平行）．
    ．

    查看答案和解析>>


    同步练习册答案