
题目列表(包括答案和解析)
下列是用代入法解方程组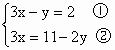 的开始步骤,其中最简单、正确的解法是
的开始步骤,其中最简单、正确的解法是
[ ]
A.由①得y=3x-2③,把③代入②得,3x=11-2(3x-2)
B.由①得x=![]() ③,把③代入②得,3×
③,把③代入②得,3×![]() =11-2y
=11-2y
C.由②得y=![]() ③,把③代入①得,3x-
③,把③代入①得,3x-![]() =2
=2
D.把②代入①得11-2y-y=2.(这种方法是把3x看做一个整体)
| 1 |
| x |
| 1 |
| x+5 |
| x-4 |
| x+5 |
 ;
; 



阅读下列解题过程,借鉴其中一种方法解答后面给出的试题:
问题:某人买13个鸡蛋,5个鸭蛋、9个鹅蛋共用去了9.25元;买2个鸡蛋,4个鸭蛋、3个鹅蛋共用去了3.20元.试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元.
分析:设买鸡蛋,鸭蛋、鹅蛋各一个分别需x、y、z元,则需要求x+y+z的值.由题意,知![]() ;
;
视![]() 为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
解法1:视![]() 为常数,依题意得
为常数,依题意得![]()
解这个关于y、z的二元一次方程组得![]()
于是![]() .
.
评注:也可以视z为常数,将上述方程组看成是关于![]() 、
、![]() 的二元一次方程组,解答方法同上,你不妨试试.
的二元一次方程组,解答方法同上,你不妨试试.
分析:视![]() 为整体,由(1)、(2)恒等变形得
为整体,由(1)、(2)恒等变形得
![]() ,
,
![]() .
.
解法2:设![]() ,
,![]() ,代入(1)、(2)可以得到如下关于
,代入(1)、(2)可以得到如下关于![]() 、
、![]() 的二元一次方
的二元一次方
程组![]()
由⑤+4×⑥,得![]() ,
,![]() .
.
评注:运用整体的思想方法指导解题.视![]() ,
,![]() 为整体,令
为整体,令![]() ,
,![]() ,代人①、②将原方程组转化为关于
,代人①、②将原方程组转化为关于![]() 、
、![]() 的二元一次方程组从而获解.
的二元一次方程组从而获解.
请你运用以上介绍的任意一种方法解答如下数学竞赛试题:
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表:
|
次数 | A1 | A2 | A3 | A4 | A5 | 总钱数 |
| 第一次购 买件数 | l | 3 | 4 | 5 | 6 | 1992 |
| 第二次购 买件数 | l | 5 | 7 | 9 | 11 | 2984 |
那么,购买每种教学用具各一件共需多少元?
(1)大桥中学初三学生对迎新文艺汇演的满意程度进行测评,评定分A、B、C、D四个等第,为了解评定情况,小明随机调查初三30名学生的学号及他们的满意度等第,结果如下:
| 学号 | 3002 | 3015 | 3039 | 3068 | 3075 | 3115 | 3132 | 3145 | 3156 | 3178 |
| 等第 | A | B | C | B | A | A | C | B | A | D |
| 学号 | 3209 | 3233 | 3251 | 3260 | 3279 | 3295 | 3313 | 3336 | 3341 | 3387 |
| 等第 | B | B | A | C | A | B | B | A | A | B |
| 学号 | 3399 | 3416 | 3452 | 3488 | 3493 | 3499 | 3501 | 3538 | 3567 | 3583 |
| 等第 | A | A | B | B | A | B | C | C | B | B |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com