
题目列表(包括答案和解析)
 与
与 之间的函数关系式及其定义域.
之间的函数关系式及其定义域.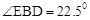 ?如果存在,求出AD的长度;如果不存在,请说明理由.
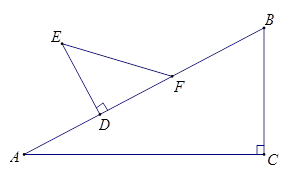
?如果存在,求出AD的长度;如果不存在,请说明理由.如图△ABC中,∠C=90°,∠A=30°,B C=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
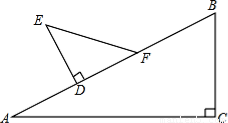
(1) 当△DEF移动至什么位置,即AD的长为多少时,E、B的连线与AC平行.
(2) 在△DEF的移动过程中,是否存在某个位置,使得∠EBD=22.5°?如果存在,求出AD的长度;如果不存在,请说明理由.

 (2014•宝山区一模)如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中,∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
(2014•宝山区一模)如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中,∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止). 如图1,一副直角三角板满足AB=BC=10,∠ABC=∠DEF=90°,∠EDF=30°,将三角板DEF的直角边EF放置于三角板ABC的斜边AC上,且点E与点A重合.
如图1,一副直角三角板满足AB=BC=10,∠ABC=∠DEF=90°,∠EDF=30°,将三角板DEF的直角边EF放置于三角板ABC的斜边AC上,且点E与点A重合.| 2 |
| 2 |
| CE |
| EA |
| CE |
| EA |
| CE |
| EA |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com