
题目列表(包括答案和解析)
如图中,判断各组中的两个三角形是否全等,并在括号内填写根据.
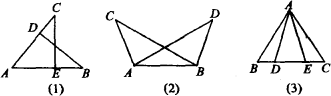
(1)如图(1),已知AB=AC,AD=AE.△AEC与△ADB.( )
(2)如图(2),已知∠BAC=∠ABD,AC=BD.△ABC与△BAD.( )
(3)如图(3),AB=AC,AD=AE,BE=DC.△AEC与△ADB.( )
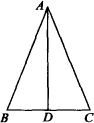
如图中,已知AB=AC,AD⊥BC,∠B=∠C.
请你猜想,BD与CD的大小关系,并试着说明理由.
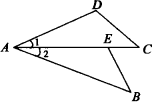
如图,若已知AB=AC,∠1=∠2,则再加上条件________(只需添加一个),就可使△ABE≌△ACD.



如图(5),已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1 ,过点A2作A2B2∥AB,A2B2交射线OM于点B2;… 依次进行下去,则A1B1线段的长度为 ,A10B10线段的长度为 .

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com