
题目列表(包括答案和解析)
看图填空.

(1)如图(1)所示,因为AB⊥AD,CD⊥AD(已知),所以______=_______=90°( ).
又因为∠1=∠2(已知),所以∠BAD-∠1=∠CDA-∠2,即∠ADF=∠DAE.所以_______∥________( ).
(2)如图(2)所示,因为BE平分∠ABD(已知),所以______=2∠1( ).因为DE平分∠BDC(已知),所以________=2∠2( ).所以______+_______=2∠1+2∠2=2(∠1+∠2).
又因为∠1+∠2=90°(已知),所以_______+_______=2×90°=180°,所以_______∥_______( ).
看图填空:
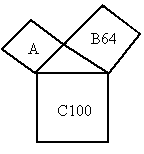
(1)如图所示,四边形A、B、C均为正方形,面积 .
.
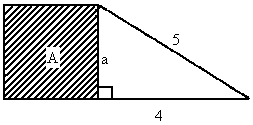
(2)如图所示,四边形A为正方形,阴影 .
.
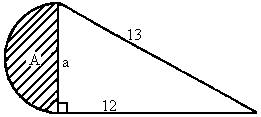
(3)如图所示,图形A为半圆,阴影 .
.
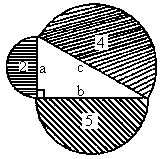
(4)如图所示,面积 (阴影部分均为半圆).
(阴影部分均为半圆).
问题情境
如图,在![]() 轴上有两点
轴上有两点![]() ,
,![]() (
(![]() ).分别过点
).分别过点![]() ,点
,点![]() 作
作![]() 轴的垂线,交抛物线
轴的垂线,交抛物线![]() 于点
于点![]() 、点
、点![]() .直线
.直线![]() 交直线
交直线![]() 于点
于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,点
,点![]() 、点
、点![]() 的纵坐标分别记为
的纵坐标分别记为![]() 、
、![]() .
.
![]()

特例探究
填空:
当![]() ,
,![]()
![]() 时,
时,![]() =____,
=____,![]() =______.当
=______.当![]() ,
,![]() 时,
时,![]() =____,
=____,![]() =______.
=______.
归纳证明
对任意![]() ,
,![]() (
(![]() ),猜想
),猜想![]() 与
与![]() 的大小关系,并证明你的猜想
的大小关系,并证明你的猜想
拓展应用.
(1) 若将“抛物线![]() ”改为“抛物线
”改为“抛物线![]() ”,其它条件不变,请直接写出
”,其它条件不变,请直接写出![]() 与
与![]() 的大小关系.
的大小关系.
(2) 连接![]() ,
,![]() .当
.当![]() 时,直接写出
时,直接写出![]() 和
和![]() 的关系及四边形
的关系及四边形![]() 的形状.
的形状.
 [
[
如图,小颖和小华两个人并排站在窗户旁,其中小颖离窗户较近.
分别画出图中两个人从窗户边缘向窗外看出去时的规视线,井比较他们从这两个位置向窗外望去时盲区的大小.
在平面内,先将一个多边形以点![]() 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为![]() ,并且原多边形上的任一点
,并且原多边形上的任一点![]() ,它的对应点
,它的对应点![]() 在线段
在线段![]() 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点![]() 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度![]() ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为![]() ,其中点
,其中点![]() 叫做旋转相似中心,
叫做旋转相似中心,![]() 叫做相似比,
叫做相似比,![]() 叫做旋转角.
叫做旋转角.
(1
)填空:①如图1,将
②如图2,![]() 是边长为
是边长为![]() 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换![]() ,得到
,得到![]() ,则线段
,则线段![]() 的长为
的长为 ![]() ;
;
(2
)如图3,分别以锐角三角形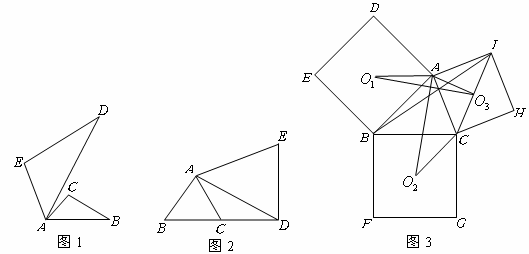
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com