亲爱的同学，你准备好了吗？让我们一起进行一次研究性学习：研究用一条直线等分几何图形的面积．我们很容易发现这样一个事实：
如图①，对于三角形ABC，取BC边的中点D，过A，D两点画一条直线，即可把△ABC分为面积相等的两部分．

（1）如图②，对于平行四边形ABCD，如何画一条直线把平行四边形ABCD分为面积相等的两部分．
答：______（写出一种方案即可）．理由是：______．
（2）受上面的启发，请你研究以下两个问题：
①如图③，一块平行四边形的稻田里有一个圆形的蓄水池，现要从蓄水池引一条笔直的水渠，并使蓄水池两侧的稻田面积相等，请你画出你的设计方案，保留作图痕迹，不必说明理由．
②某农业研究所有一块梯形形状的实验田如图3④，准备把这块实验田种上面积相同的西红柿和青椒（都是新品种），应该如何分割，请你分别在图3④、图3⑤中设计两种不同的分割方案，并说明理由．

同学们会玩五子棋的游戏吗？五子棋和围棋一样，深受广大棋友的喜爱，它的比赛规则是：在正方形棋盘中，由黑方先行，轮流弈子，只要一方首先在任一方向上将5个同色子连成一条直线（中间无间隔）就算赢，如图(1）或图(2)所示. 甲、乙两人在玩一盘棋，两人下到第七步时的情况如图(3）所示，

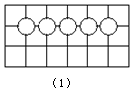
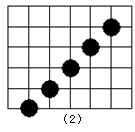
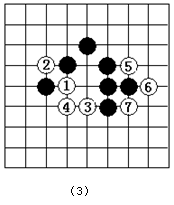
1.若每个小正方形的边长为1个单位长度，请在图中建立适当的平面直角坐标系，使棋子白④的位置是（1，－2），并写出棋子白⑥的坐标

2.若现在轮到甲走黑棋，甲下在哪里就会必胜？请在已经建立的平面直角坐标系下写出三个符合条件的点的坐标.