
题目列表(包括答案和解析)
 ),若线段RS绕原点O逆时针旋转90°,求线段RS所经过区域的面积(重复经过的区域面积不重复计算).
),若线段RS绕原点O逆时针旋转90°,求线段RS所经过区域的面积(重复经过的区域面积不重复计算).

| 1 |
| 2 |
| 1 |
| 2 |
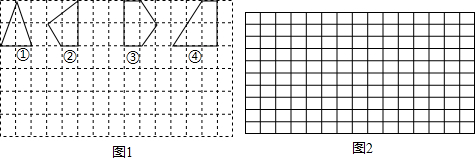
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | … |
| 1 |
| 2 |
| 1 |
| 2 |
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | … |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com