(2007•临夏州)[(1)-(3),10分]如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h
1、h
2、h
3,△ABC的高为h.
在图(1)中,点P是边BC的中点,此时h
3=0,可得结论:h
1+h
2+h
3=h.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中,h
1、h
2、h
3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60°,RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h
1、h
2、h
3、h
4,桥形的高为h,则h
1、h
2、h
3、h
4、h之间的关系为:
m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h
m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h
;图(4)与图(6)中的等式有何关系?


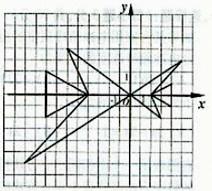 16、如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为
16、如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为

