设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．

（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下

表：(6分)

所以，

当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；

（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：(5分)

所以，当r＝a时，⊙O与正方形的公共点个数可能有　　　　　个；

（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；(5分)

设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．

（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下

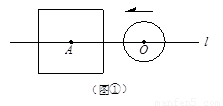
表：(6分)

所以，

当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；

（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：(5分)

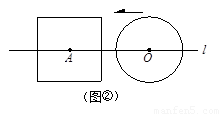
所以，当r＝a时，⊙O与正方形的公共点个数可能有　　　　　个；

（3）如图③，当⊙O与正方形有5个公共点时，试说明r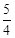＝a；(5分)

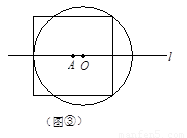
设边长为2a的正方形的中心A在直线L上，它的一组对边垂直于直线L，半径为r的⊙O的圆心O在直线L上运动，点A，O间距离为d．

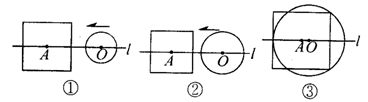
    （1）如图3－3－17①，当r<a时，根据d与a，r之间关系，将⊙O与正方形的公共点个数填入下表：

    所以，当r<a时，⊙O与正方形的公共点的个数可能有_______个．

    （2）如图3－3－17②，当r=a时，根据d与a，r之间关系，将⊙O与正方形的公共点个数填入下表：

    所以，当r=a时，⊙O与正方形的公共点个数可能有______个．

    （3）如图3－3－17③，当⊙O与正方形有5个公共点时，试说明r=a；

（4）就r>a的情形，请你仿照“当……时，⊙O与正方形的公共点个数可能有_____个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．

设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．

(1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：

所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；

(2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：

所以，当r＝a时，⊙O与正方形的公共点个数可能有　　　　　　　　个；

(3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；

(4）就r＞a的情形，请你仿照摰薄??保??I>O与正方形的公共点个数可能有

　　　　　　 个數男问剑?辽俑?鲆桓龉赜趽⊙O与正方形的公共点个数數恼?方崧郏?ㄗⅲ旱冢?）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）