
题目列表(包括答案和解析)
看图填空.

(1)如图(1)所示,因为AB⊥AD,CD⊥AD(已知),所以______=_______=90°( ).
又因为∠1=∠2(已知),所以∠BAD-∠1=∠CDA-∠2,即∠ADF=∠DAE.所以_______∥________( ).
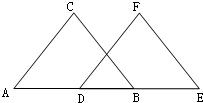
(2)如图(2)所示,因为BE平分∠ABD(已知),所以______=2∠1( ).因为DE平分∠BDC(已知),所以________=2∠2( ).所以______+_______=2∠1+2∠2=2(∠1+∠2).
又因为∠1+∠2=90°(已知),所以_______+_______=2×90°=180°,所以_______∥_______( ).
看图填空:
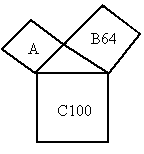
(1)如图所示,四边形A、B、C均为正方形,面积 .
.
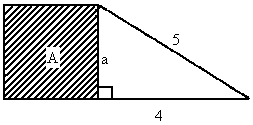
(2)如图所示,四边形A为正方形,阴影 .
.
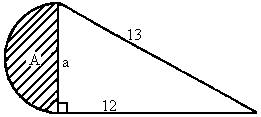
(3)如图所示,图形A为半圆,阴影 .
.
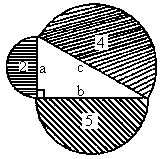
(4)如图所示,面积 (阴影部分均为半圆).
(阴影部分均为半圆).
 20、看图填空:
20、看图填空: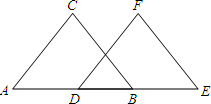 看图填空:
看图填空:
|
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y=x2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … | |||
| y=(x+3)2 | … | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | ▲ | … |
| k |
| x-m |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com