
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
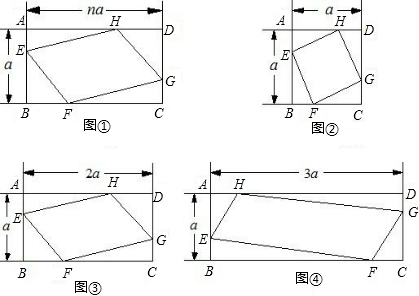
(本题10分)已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
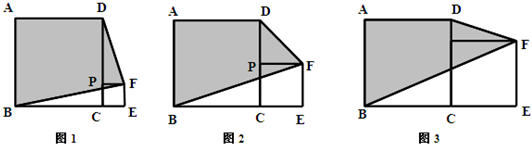
1.观察计算:(1)如图1,当a=4,b=1时,四边形ABFD的面积为 ;
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 ;
2.探索发现:(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;
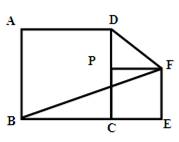
3.综合应用:(5)农民赵大伯有一块正方形的土地(如图),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.(要求尺规作图,保留作图痕迹)

(本题满分9分)
如图,以为顶点的抛物线与
轴交于点
.已知
、
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设是抛物线上的一点(
、
为正整数),且它位于对称轴的右侧.若以
、
、
、
为顶点的四边形四条边的长度是四个连续的正整数,求点
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点,
![]() 是否总成立?请说明理由.
是否总成立?请说明理由.
 为顶点的抛物线与
为顶点的抛物线与 轴交于点
轴交于点 .已知
.已知 、
、 两点坐标分别为(3,0)、(0,4).
两点坐标分别为(3,0)、(0,4). 是抛物线上的一点(
是抛物线上的一点( 、
、 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以 、
、 、
、 、
、 为顶点的四边形四条边的长度是四个连续的正整数,求点
为顶点的四边形四条边的长度是四个连续的正整数,求点 的坐标;
的坐标; ,
, 是否总成立?请说明理由.
是否总成立?请说明理由.
(本题满分9分)
如图,以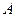 为顶点的抛物线与
为顶点的抛物线与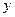 轴交于点
轴交于点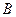 .已知
.已知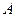 、
、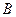 两点坐标分别为(3,0)、(0,4).
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设 是抛物线上的一点(
是抛物线上的一点(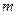 、
、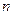 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以 、
、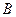 、
、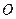 、
、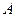 为顶点的四边形四条边的长度是四个连续的正整数,求点
为顶点的四边形四条边的长度是四个连续的正整数,求点 的坐标;
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点 ,
,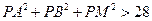 是否总成立?请说明理由.
是否总成立?请说明理由.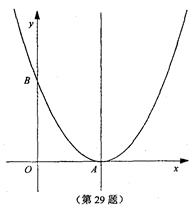
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com