在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：
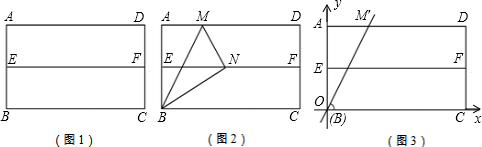
第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；
第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）．
请解答以下问题：
（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论；
（2）在图2中，若AB=a，BC=b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP？
（3）设矩形ABCD的边AB=2，BC=4，并建立如图3所示的直角坐标系．设直线BM′为y=kx，当∠M′BC=60°时，求k的值．此时，将△ABM′沿BM′折叠，点A是否落在EF上（E、F分别为AB、CD中点），为什么？

聪明好学的小云查阅有关资料发现：用不过圆锥顶点平行于一条母线的平面截圆锥所得的截面为抛物面，即图1中曲线CFD为抛物线的一部分，如图1，圆锥体SAB的母线长为10，侧面积为50π，圆锥的截面CFD交母线SB于F，交底面⊙P于C、D，AB⊥CD于O，OF∥SA且OF⊥CD，OP=4，OB=9．
（1）求底面圆的半径AP的长及圆锥侧面展开图的圆心角的度数；
（2）当以CD所在直线为x轴，OF所在的直线为y轴建立如图2所示的直角坐标系，求过C、F、D三点的抛物线的函数关系式．