运用乘法公式计算：
（1）（2m-3n）（-2m-3n）-（2m-3n）²
（2）100²-99²+98²-97²+…+2²-1²．

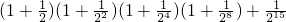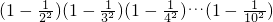某同学在计算3（4+1）（4²+1）时，把3写成4-1后，发现可以连续运用平方差公式计算：3（4+1）（4²+1）=（4-1）（4+1）（4²+1）=（4²-1）（4²+1）=16²-1．很受启发，后来在求（2+1）（2²+1）（2⁴+1）（2⁸+1）…（2²⁰⁴⁸+1）的值时，又改造此法，将乘积式前面乘以1，且把1写为2-1得（2+1）（2²+1）（2⁴+1）（2⁸+1）…（2²⁰⁴⁸+1）=（2-1）（2+1）（2²+1）（2⁴+1）（2⁸+1）…（2²⁰⁴⁸+1）=（2²-1）（2²+1）（2⁴+1）（2⁸+1）…（2²⁰⁴⁸+1）=（2⁴-1）（2⁸+1）…（2²⁰⁴⁸+1）=（2²⁰⁴⁸-1）（2²⁰⁴⁸+1）=2⁴⁰⁹⁶-1
回答下列问题：
（1）请借鉴该同学的经验，计算：；
（2）借用上面的方法，再逆用平方差公式计算：．

我们在计算（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）（2³²+1）时，发现直接运算很麻烦，如果在算式前乘以（2－1），即1，原算式的值不变，而且还使整个算式能用乘法公式计算．解答过程如下：

原式=（2－1）（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）（2³²+1）

=（2²－1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）（2³²+1）

=（2⁴－1）（2⁴+1）（2⁸+1）（2¹⁶+1）（2³²+1）

=……=2⁶⁴－1

你能用上述方法算出（3+1）（3²+1）（3⁴+1）（3⁸+1）（3¹⁶+1）的值吗？请试试看!

综合提高