阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣。

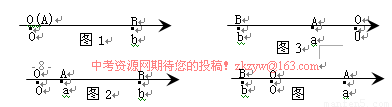
当A、B两点中有一点在原点时，不妨设点A在原点，

如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；

当A、B两点都不在原点时，

如图2，点A、B都在原点的右边

∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣；

如图3，点A、B都在原点的左边，

∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=－b-（-a）=∣a-b∣；

如图4，点A、B在原点的两边，

∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣= a +（-b）=∣a-b∣；

回答下列问题：

（1）数轴上表示2和5的两点之间的距离是_________,数轴上表示－2和－5的两点之间的距离是_________,数轴上表示1和－3的两点之间的距离是_______；

（2）数轴上表示x和－1的两点A和B之间的距离是___________,如果∣AB∣＝2，那么x为____________；

（3）当代数式∣x+1∣＝∣x-2∣取最小值时，相应的x的取值范围是             .

小明对直角三角形很感兴趣. △ABC中，∠ACB＝90°，D是AB上任意一点，连接DC，作DE⊥DC，EA⊥AC，DE与AE交于点E.请你跟着他一起解决下列问题：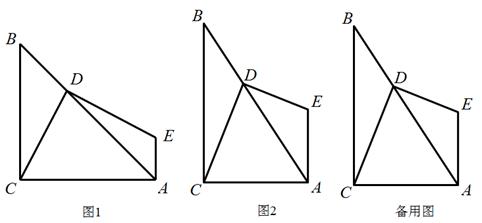

(1)如图1，若△ABC是等腰直角三角形，则DE,DC有什么数量关系？请给出证明.
(2)如果换一个直角三角形，如图2，∠CBA＝30°，则DE,DC又有什么数量关系？请给出证明.
(3)由(1)、(2)这两种特殊情况，小明提出问题：如果直角三角形ABC中，BC=mAC，那DE, DC有什么数量关系？请给出证明.

如图，抛物线y＝ax²＋bx＋c的顶点为P，对称轴直线x＝1与x轴交于点D，抛物线与x轴交于A、B两点，与y轴交于点C，其中A（－1，0）、C(0，3)．
【小题1】求此抛物线的解析式
【小题2】点E在线段BC上，若△DEB为等腰三角形，求点E的坐标
【小题3】点F、Q都在该抛物线上，若点C与点F关于直线x＝1成轴对称，连结BF、BQ，如果∠FBQ＝45°，求点Q的坐标；
【小题4】将△BOC绕着它的顶点B顺时针在第一象限内旋转，旋转后的图形为△BO'C'，BO'与BP重合时，则△BO'C'不在BP上的顶点C'的坐标为   ▲   （直接写出答案）．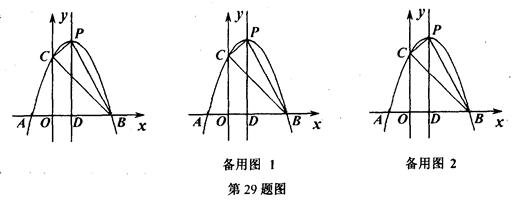

（1）阅读下面材料：

点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣。当A、B两点中有一点在原点时，不妨设点A在原点，如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；当A、B两点都不在原点时，如图2，点A、B都在原点的右边∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=b-a=∣a-b∣；

①  如图3，点A、B都在原点的左边，∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=－b-（-a）=∣a-b∣；

②  如图4，点A、B在原点的两边,∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣= a +（-b）=∣a-b∣；

（2）回答下列问题：

1.数轴上表示2和5的两点之间的距离是_________,数轴上表示－2和－5的两点之间的距离是_________,数轴上表示1和－3的两点之间的距离是_______；（共3分）

2.数轴上表示x和－1的两点A和B之间的距离是_____,如果∣AB∣＝2，那么x为_  ___  （共4分）

3.当代数式∣x+1∣+∣x-2∣+∣x+3∣取最小值时，相应的x的值是___________;此时代数式∣x+1∣+∣x-2∣+∣x+3∣的值是_____________.（6分）

如图，抛物线y＝ax²＋bx＋c的顶点为P，对称轴直线x＝1与x轴交于点D，抛物线与x轴交于A、B两点，与y轴交于点C，其中A（－1，0）、C(0，3)．

1.求此抛物线的解析式

2.点E在线段BC上，若△DEB为等腰三角形，求点E的坐标

3.点F、Q都在该抛物线上，若点C与点F关于直线x＝1成轴对称，连结BF、BQ，如果∠FBQ＝45°，求点Q的坐标；

4.将△BOC绕着它的顶点B顺时针在第一象限内旋转，旋转后的图形为△BO'C'，BO'与BP重合时，则△BO'C'不在BP上的顶点C'的坐标为    ▲    （直接写出答案）．