
题目列表(包括答案和解析)
(1)x的4倍减去2后,比x的3倍大5,求x;
(2)某数与2的和乘以5,仍等于这个数,求这个数;
(3)某数的3倍与-5的差等于这个数的2倍的相反数,求这个数;
(4)七年级共有学生550人,其中男生比女生多10人,求女生的人数;
(5)一个长方形的长比宽多2 cm,若把它的长和宽分别增加2 cm后,面积则增加16 cm2,求原来长方形的宽.
| 月份x | 1月 | 2月 | 3月 | 6月 |
| 月销量p(单位:棵) | 500 | 600 | 700 | 1000 |
| 203 |
| 205 |
| 206 |
| 月份x | 1月 | 2月 | 3月 | 6月 |
| 月销量p(单位:棵) | 500 | 600 | 700 | 1000 |
 )
)| 月份x | 1月 | 2月 | 3月 | 6月 |
| 月销量p(单位:棵) | 500 | 600 | 700 | 1000 |
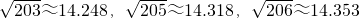 )
)| 月份x | 1月 | 2月 | 3月 | 6月 |
| 月销量p(单位:棵) | 500 | 600 | 700 | 1000 |
| 203 |
| 205 |
| 206 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com