在y轴上且到点A(4，0)的线段长度为5的点B的坐标是．

A．(0，3)

B．(0，－3)

C．(0，3)或(0，－3)

D．(3，0)或(－3，0)

某旅游胜地欲开发一座景观山．从山的侧面进行堪测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位：百米)．已知AB所在抛物线的解析式为y＝－x²＋8，BC所在抛物线的解析式为y＝(x－8)²，且已知B(m，4)．

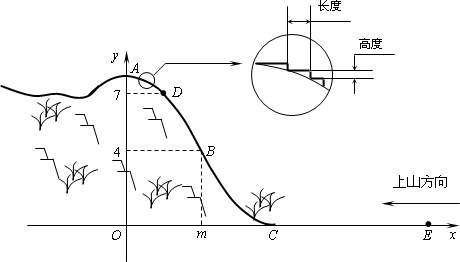
(1)设P(x，y)是山坡线AB上任意一点，用y表示x，并求点B的坐标；

(2)从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为20厘米，长度因坡度的大小而定，但不得小于20厘米，每级台阶的两端点在坡面上(见图)．

①分别求出前三级台阶的长度(精确到厘米)；

②这种台阶不能一直铺到山脚，为什么？

(3)在山坡上的700米高度(点D)处恰好有一小块平地，可以用来建造索道站．索道的起点选择在山脚水平线上的点E处，OE＝1600(米)．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为y＝(x－16)²．试求索道的最大悬空高度．

如图，在平面直角坐标系中，顶点为(4，－1)的抛物线交Y轴于A点，交X轴于B，B两点(点B在点C的左侧)， 已知a点坐标为(0，3).

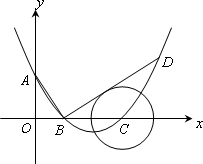
(1)求此抛物线的解析式；

(2)过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴L与⊙C有怎样的位置关系，并给出证明；

(3)已知点P是抛物线上的一个动点，且位于A，C两点之间，过点P作Y轴的平行线与AC交于点Q问：当点P运动到什么位置时，线段PQ的长度最大？并求出此时△PAC的面积

在平面直角坐标系中，已知M₁(3，2)，N₁(5，－1)，线段M₁N₁平移至线段MN处(注：M₁与M，N₁与N分别为对应点)．

(1)若M(－2，5)，请直接写出N点坐标．

(2)在(1)问的条件下，点N在抛物线上，求该抛物线对应的函数解析式．

(3)在(2)问条件下，若抛物线顶点为B，与y轴交于点A，点E为线段AB中点，点C(0，m)是y轴负半轴上一动点，线段EC与线段BO相交于F，

且OC∶OF＝2∶，求m的值．

(4)在(3)问条件下，动点P从B点出发，沿x轴正方向匀速运动，点P运动到什么位置时(即BP长为多少)，将△ABP沿边PE折叠，△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的，求此时BP的长度．