
题目列表(包括答案和解析)
如图13,已知EF⊥BC,∠1=∠C,∠2+∠3=180°. 试说明直线AD与BC垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:
∵ ∠1=∠C, ( 已知 )
∴ ∥ ,( )
∴ ∠2= . ( )
又∵ ∠2+∠3=180°,( 已知 )
∴ ∠3+ =180°.( 等量代换 )
∴ ∥ , ( )
∴ ∠ADC=∠EFC. ( )
∵ EF⊥BC, ( 已知 )
∴ ∠EFC=90°,
∴ ∠ADC=90°,
∴ ⊥ .
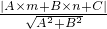 .
.
 x-
x- 的距离d时,先将y=
的距离d时,先将y=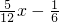 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=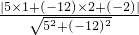 =
= .
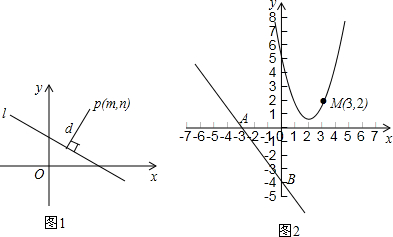
. 与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).小明、![]() 小亮、小刚、小颖一起研究一道数学题.如图7-20,已知EF⊥AB,CD⊥AB,
小亮、小刚、小颖一起研究一道数学题.如图7-20,已知EF⊥AB,CD⊥AB,
小明说:“如果还知道∠CD![]() G=∠BFE,则能得到∠AGD=∠ACB.”
G=∠BFE,则能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结![]() 论倒过来,即由∠AGD=∠ACB,
论倒过来,即由∠AGD=∠ACB,
可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,则GF一定平行于AB.”
他们四人中,有_________________个人的说法是正确的.
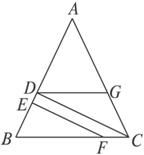
图7-20
A.1 B.2 C.3 D.4
如图13,已知EF⊥BC,∠1=∠C,∠2+∠3=180°. 试说明直线AD与BC垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
理由:
∵ ∠1=∠C, ( 已知 )
∴ ∥ ,( )
∴ ∠2=" " . ( )
又∵ ∠2+∠3=180°,( 已知 )
∴ ∠3+ =180°.( 等量代换 )
∴ ∥ , ( )
∴ ∠ADC=∠EFC. (  )
)
∵ EF⊥BC, ( 已 知 )
知 )
∴ ∠EFC=90°,
∴ ∠ADC=90°,
∴ ⊥ .

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com