
题目列表(包括答案和解析)
阅读下列材料,按要求解答问题:
如图2-1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通过以下计算:由题意,∠B=30°,∠C=90°,c=2b,a=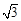 b,得a2-b2=(
b,得a2-b2=(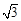 b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.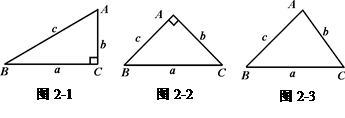
于是,小明猜测:对于任意的ΔABC,当∠A=2∠B时,关系式a2-b2=bc都成立.
(1)如图2-2,请你用以上小明的方法,对等腰直角三角形进行验证,判断小明的猜测是否正确,并写出验证过程;
(2)如图2-3,你认为小明的猜想是否正确,若认为正确,请你证明;否则,请说明理由;
(3)若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
阅读下面的情境对话,然后解答问题
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt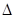 ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt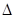 ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
1求证: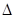 ACE是奇异三角形;
ACE是奇异三角形;
2当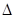 ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
如图,在Rt△ABC中,∠BAC=90º,若AB=3cm,BC=5cm,E在AB上且AE=1cm,点P从B点出发,以1cm/s的速度沿BC→CA运动至A点停止,设运动的时间为ts,当t= ,△BEP为等腰三角形。
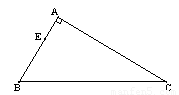
如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC ,AD=2cm,AB=8cm,CD=10cm.
(1)求梯形ABCD的周长;
(2)动点P从点B出发,以1cm/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以1cm/s的速度沿C→D→A方向向点A运动;过点Q作QF⊥BC于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之结束,设运动时间为t秒.问:
在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
如图,□ABCD中,AB=4,BC=3,∠BAD=120°,动点E在BC上(不与B
重合).作EF⊥AB于F,FE、DC的延长线交于点G.设BE=x,△DEF的面积为S.
1.求S关于x的函数表达式,并写出x的取值范围
2.当点E在何处时,S有最大值,最大值为多少?
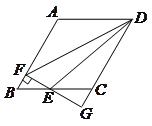
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com