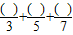有一个算式分子都是整数，满足≈1.16，那么你能算出他们的分子依次是哪些数吗？
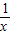在我们的教科书中选取了一些具体值并将它们代入要解的一元二次方程中，大致估计出一元二次方程解的范围，再在这个范围内逐步加细赋值，进而逐步估计出一元二次方程的近似解．下面介绍另外一种估计一元二次方程近似解的方法，以方程x²-3x-1=0为例，因为x≠0，所以先将其变形为x=3+，用3+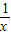代替x，得x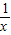=3+=3+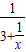．反复若干次用3+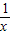代替x，就得到x=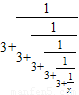形如上式右边的式子称为连分数．
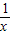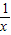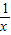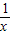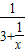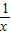可以猜想，随着替代次数的不断增加，右式最后的对整个式子的值的影响将越来越小，因此可以根据需要，在适当时候把忽略不计，例如，当忽略x=3+中的时，就得到x=3；当忽略x=3+中的时，就得到x=3+；如此等等，于是可以得到一系列分数；
3，3+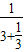，3+，3+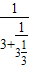，…，即3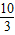，=3.3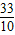33…，≈3.3.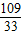=3.303 03…，…．
可以发现它们越来越趋于稳定，事实上，这些数越来越近似于方程x²-3x-1=0的正根，而且它的算法也很简单，就是以3为第一个近似值，然后不断地求倒数，再加3而已，在计算机技术极为发达的今天，只要编一个极为简单的程序，计算机就能很快帮你算出它的多个近似值．

我国著名数学家华罗庚曾说过：撌?毙问鄙僦惫郏?紊偈?蹦讶胛ⅲ皇?谓岷习侔愫茫?衾敕旨彝蚴滦輸．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．

数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．

例如，求1＋2＋3＋4＋…＋n的值，其中n是正整数．

对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．

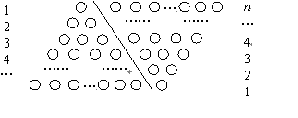
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1＋2＋3＋4＋…＋n 的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1＋2＋3＋4＋…＋n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有（n＋1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n＋1）个，因此，组成一个三角形小圆圈的个数为，即1＋2＋3＋4＋…＋n＝．

(1）仿照上述数形结合的思想方法，设计相关图形，求1＋3＋5＋7＋…＋（2n－1）的值，其中 n 是正整数．（要求：画出图形，并利用图形做必要的推理说明）

(2）试设计另外一种图形，求1＋3＋5＋7＋…＋（2n－1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）

（32分）古今中外，无数的仁人志士强调关注民生，维护人性尊严，提倡宽容，反对暴力，主张自由平等和自我价值的体现。阅读下列材料：
材料一  从此观之，财之与势，固英雄之所必资，而大圣人之所必用也，何可言无也?吾故曰，虽大圣人不能无势利之心。则知势利之心，亦吾人秉赋之“自然”矣。    
——《李氏（贽）文集》卷一
材料二  对于全国人民之食衣住行四大需要，政府当与人民协力，共谋农业之发展，以足民食；共谋织造之发展，以裕民衣；建筑大计划之各式屋舍，以乐民居；修治道路、运河，以利民行……每县开创自治之时，必须先规定全县私有土地之价，其法由地主自报之，地方政府则照价征税，并可随照价收买……土地之岁收，地价之增益，公地之生产，山林川泽之息，矿产水力之利，皆为地方政府之所有，而用以经营地方人民之事业……各县之天然富源及大规模之工商事业，本县之资力不能发展与兴办，而须外资（指外地资本）乃能经营者，当由中央政府为之协助。  ——孙中山《国民政府建国大纲》
材料三  我们不要四面出击。四面出击，全国紧张，很不好。绝不可树敌太多，必须在一个方面有所让步，有所缓和，……我们一定要做好工作，使工人、农民、小手工业者都拥护我们，使民族资产阶级和知识分子中的绝大多数不反对我们。 ——毛泽东《不要四面出击》
材料四  社会给予他们的委托以及上帝和自然法对各种政体的国家机关的权力所定的界限：第一，它们应当以正式公布的固定法律进行统治，这些法律不论贫富、不论宫廷权贵和乡村农夫都一视同仁，不因特殊情况而有所改变。第二，这些法律知识为了人民的福利这一最终目的，此外不应再有其他目的。第三，未经人民自己或其代表同意，决不能对人民的财产课税。第四，（立法权和执行权该由不同的人员行使，法官应该独立。）立法机关既不应该也不能把制定法律的权力转让给其他任何人，也不能把它置于并非人民安排的其他任何地方。   ——洛克《政府论》
（1）材料一所述思想主张产生的社会根源是什么?（4分）
（2）依据材料二，概括孙中山建国大纲的主要主张（不得摘抄原文）。（6分）
（3）结合所学知识，概括指出20世纪30年代初期，我们是怎样使农民、小手工业者都拥护我们的?建国初期，我们又是怎样使民族资产阶级中的大多数不反对我们的（12分）
（4）依据材料四，概括指出洛克的主要思想主张。（10分）