
题目列表(包括答案和解析)
据我国古代《周髀算经》记载,公元前1120年,商高对周公说:“将一根直尺折成一个直角,两端连结得一个直角三角形,如果勾是三,股是四,那么弦就等于五.”后人概括为:“勾三、股四、弦五.”
(1)观察3、4、5;5、12、13;7、24、25;….可以发现这几组勾股数的“勾”都是奇数,且从3起就没有间断过.计算![]() (9-1),
(9-1),![]() (9+1)与
(9+1)与![]() (25-1),
(25-1),![]() (25+1),并根据你发现的规律,分别写出能(用勾)表示7、24、25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能(用勾)表示7、24、25的股和弦的算式;
(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦.猜想它们之间的两种相等关系,并对猜想加以说明;
(3)继续观察4、3、5;6、8、10;8、15、17;….可以发现各组的第一个数都是偶数,且从4起也没有间断过,运用类似上述探索的方法,直接用m(m为偶数且m≥4)的代数式来表示它们的股和弦.
据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连结得一个直角三角形,如果勾是三、股是四,那么弦就等于五.后人概括为摴慈?⒐伤摹⑾椅鍞.
(1) 观察:3,4,5;5,12,13;7,24,25;···,发现这些勾股数的勾都是奇数,且从3起就没有间断过.计算![]() 与
与![]() ,并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
,并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(2) 根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合情猜想他们之间二种相等关系并对其中一种猜想加以证明;
(3) 继续观察4,3,5;6,8,10;8,15,17;···,可以发现各组的第一个数都是偶数,且从4起也没有间断过.运用类似上述探索的方法,直接用m(m为偶数且m>4)的代数式来表示他们的股和弦.
考生注意:除第(2)小题中已发现的相等关系之外,你还有其他新的发现,并能正确证明,将酌情另加分.
我区某镇地理环境偏僻,严重制约经济发展,丰富的花木产品只能在本地销售,我区政府对该花木产品每投资![]() 万元,所获利润为
万元,所获利润为![]() ,为了响应我国西部大开发的宏伟决策,我区政府在制定经济发展的10年规划时,拟开发此花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路,且5年修通.公路修通后,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每投资x万元可获利润
,为了响应我国西部大开发的宏伟决策,我区政府在制定经济发展的10年规划时,拟开发此花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路,且5年修通.公路修通后,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每投资x万元可获利润![]()
⑴若不进行开发,求10年所获利润的最大值是多少?
⑵若按此规划进行开发,求10年所获利润的最大值是多少?
⑶根据⑴、⑵计算的结果,请你用一句话谈谈你的想法.
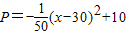 万元.为了响应我国西部大开发的宏伟决策,镇政府在制定经济发展的10年规划时,拟定开发花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路;后5年公路修通时,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每年固定投资x万元可获利润
万元.为了响应我国西部大开发的宏伟决策,镇政府在制定经济发展的10年规划时,拟定开发花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路;后5年公路修通时,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每年固定投资x万元可获利润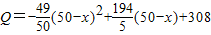 万元.
万元.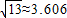 ,
,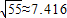 ,计算结果保留1位小数)
,计算结果保留1位小数) 万元.为了响应我国西部大开发的宏伟决策,镇政府在制定经济发展的10年规划时,拟定开发花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路;后5年公路修通时,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每年固定投资x万元可获利润
万元.为了响应我国西部大开发的宏伟决策,镇政府在制定经济发展的10年规划时,拟定开发花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路;后5年公路修通时,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每年固定投资x万元可获利润 万元.
万元. ,
, ,计算结果保留1位小数)
,计算结果保留1位小数)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com