已知抛物线y=2x2，⊙O与抛物线交于A、B两点，AB两点所在的直线为l，⊙O的半径为2。
（1）当x＞xB时，抛物线上存在一动点C，则随着C点的向上运动，三角形ABC面积不断增加，问三角形ABC面积每秒的增加量△S是什么？（友情提醒：C点的速度为v0·s-1）；
（2）存在一点D在劣弧AB上运动（不与A、B重合）设D（h，k），问抛物线上是否存在点E使得三角形ABD与三角形ABE的面积相等？若存在，求出点E；若不存在，请说明理由；
（3）F（m，n）（m＞0）是抛物线y=2x2上的点，OF⊥FG，G（a，0）（a＞m），△OFG的面积为S，且S=4n4，n是不大于40的整数，求OF2的最小值；
（4）在抛物线上取两点J、K，xJ＜0，xk＞0，连接OJ、JK、OK，使得角OKJ=60°，再以OK、OJ、JK分别作等边三角形OKL、OJM、OKN，请你求出经过M、N、L三点的抛物线的解析式。
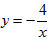的图象上的三个点，且x1＜x2＜0，x3＞0，则y1，y2，y3的大小关系是（ ）。