
题目列表(包括答案和解析)
| |||||
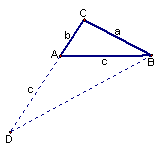
在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图23-1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.
 | |||||||
 | |||||||
 | |||||||
 | |||||||
(图23-1) (图23-2) (图23-3) (图23-4)
(1)我们先从特殊的倍角三角形入手研究。请你结合图形填空:
三角形 | 角的已知量 |
|
|
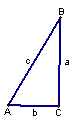
图23-2 | ∠A=2∠B= | ||
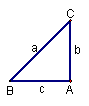
图23-3 | ∠A=2∠B= |
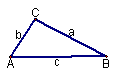
(2)如图23-4,对于一般的![]() 倍角△ABC,若∠CAB=2∠CBA ,∠CAB、∠CBA、∠C的对边分别记为a,b,c,a,b,c,三边有什么关系呢?请你作出猜测,并结合图23-4给出的辅助线提示加以证明.
倍角△ABC,若∠CAB=2∠CBA ,∠CAB、∠CBA、∠C的对边分别记为a,b,c,a,b,c,三边有什么关系呢?请你作出猜测,并结合图23-4给出的辅助线提示加以证明.
(3)请你运用(2)中的结论解决下列问题:若一个倍角三角形的两边长为5,6,求第三边长. (直接写出结论即可)(原创)


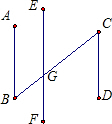 填空:
填空:推理填空:
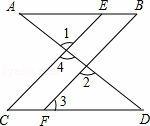
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ C =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com