
题目列表(包括答案和解析)
“黑洞”是恒星演化的最后阶段.根据有关理论,当一颗恒星衰老时,其中心的燃料(氢)已经被耗尽,在外壳的重压之下,核心开始坍(tān)缩,直到最后形成体积小、密度大的星体.如果这一星体的质量超过太阳质量的三倍,那么就会引发另一次大坍缩.当这种收缩使得它的半径达到施瓦氏(Schwarzs-child)半径后,其引力就会变得相当强大,以至于光也不能逃脱出来,从而成为一个看不见的星体——黑洞.施瓦氏半径(单位:米)的计算公式是
 ,
,
其中 牛·
牛· /
/ ,为万有引力常数;M表示星球的质量(单位:千克);
,为万有引力常数;M表示星球的质量(单位:千克); 米/秒,为光在真空中的速度.
米/秒,为光在真空中的速度.
已知太阳的质量为 千克,半径为700000千米,计算太阳的施瓦氏半径并估计这两个球体的相对大小.
千克,半径为700000千米,计算太阳的施瓦氏半径并估计这两个球体的相对大小.
一次数学兴趣小组的活动课上,师生有下面的一段对话,请你阅读完后再解答.
老师:同学们,今天我们来探索如下方程的解法:
![]() .
.
学生甲:老师,这个方程先去括号,在合并同类项,行吗?
老师:这样原方程可整理为![]() ,次数变成了4次,用现有的知识无法解答.同学们再观察,看看这个方程有什么特点?
,次数变成了4次,用现有的知识无法解答.同学们再观察,看看这个方程有什么特点?
学生乙:老师,我发现方程中![]() 是整体出现的,最好不要去括号!
是整体出现的,最好不要去括号!
教师:很好,我国我们把![]() 看成一个整体,用
看成一个整体,用![]() 表示,即
表示,即![]() ,那么原方程就变成了
,那么原方程就变成了![]() .
.
全体学生:(同学们都特别高兴)噢,这不是我们最熟悉的一元二次方程吗?
老师:大家真会观察和思考,太棒了!显然一元二次方程![]() 的根是
的根是![]() ,
,![]() ,那么就有
,那么就有![]() 或
或![]() .
.
学生丙:对啦,再解这两个方程,可得原方程的根是![]() ,
,![]() ,
,![]() ,
,![]() .嗬,有这么多解啊!
.嗬,有这么多解啊!
老师:同学们,通常我们把这种方法叫做换元法.在这里,使用它最大的妙处在于降低方程的次数,这是一种重要的转化方法.
全体学生:OK,换元法真神奇!
现在,请你用换元法解下列分式方程:
![]()
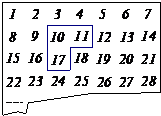 有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所
有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所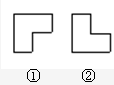 给示例),设被框住的三个数中最小的数为a.
给示例),设被框住的三个数中最小的数为a. 有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所
有两个如图所示的曲尺形框,框①和框②,用它们分别可以框住下表中的三个数(如图所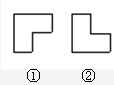 给示例),设被框住的三个数中最小的数为a.
给示例),设被框住的三个数中最小的数为a.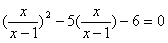
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com