
题目列表(包括答案和解析)
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如撏?资?莸某朔ǚㄔ驍的学习过程是利用有理数的乘方概念和乘法结合律,由撎厥鈹到撘话銛进行抽象概括的:![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
![]()
![]()
我们亦知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1
)请你根据上面的材料归纳出(2
)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:撊-(3
)如图,在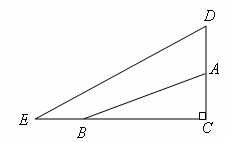
| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
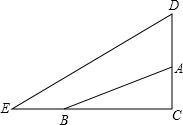 同的关系式并给予证明.
同的关系式并给予证明.| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com