对于有理数a、b，有以下几种说法，其中正确的说法个数是
①若a+b=0，则a与b互为相反数；②若a+b＜0，则a与b异号；③a+b＞0，则a与b同号时，则a＞0，b＞0；④|a|＞|b|且a、b异号，则a+b＞0；⑤|a|＜b，则a+b＞0．

上课时老师提出一个问题：如果有两组牌，它们的牌面数字分别是1，2，3，那么从每组牌中各摸出一张牌，

问：两张牌的牌面数字之和为几的概率最大？最大概率是多少？

小明、小颖、小亮三名同学分别进行了如下的求解过程．

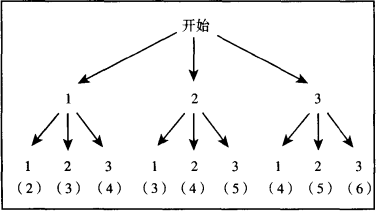
小明的做法：

我借助于树状图，从树状图可以发现：总共有9种情况，每种情况发生的可能性相同，而两张牌的牌面数字和等于4的情况出现得最多，共3次，因此牌面数字和等于4的概率最大，概率为，即．

小颖的做法：

我通过列下表得到牌面数字之和等于4的概率最大，概率为．

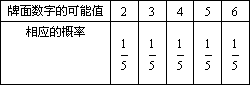
小亮的做法：

我也用了列表的方法，可我得到牌面数字之和等于4的概率为．

你认为谁做得对？请说说你的理由．