我们知道过n边形的一个顶点可以做（n-3）条对角线，这（n-3）条对角线把三角形分割成（n-2）个三角形，想一想这是为什么？如图1．
如图2，在n边形的边上任意取一点，连接这点与各顶点的线段可以把n边形分成几个三角形？
想一想，利用这两个图形，怎样证明多边形的内角和定理．
．

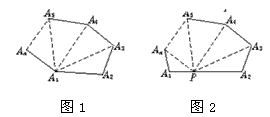
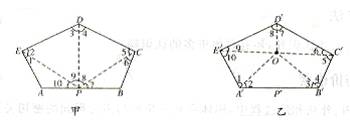
甲：在五边形ABCDE的边AB上取一点P，连结PC、PD、PE，则有

又∵，∴，

即。

乙：在五边形A′B′C′D′E′的内部任取一点O，连结OA′、OB′、OC′、OD′、OE′，则有（ A′O E′）＋（ A′O B′）＋（ B′O C′）＋（ C′O D′）＋（ D′O E′）＝900

又∵ A′O E′+ A′O B′+ B′O C′+ C′O D′+ D′O E′＝360，

∴，

即 E′A′B′+ A′B′C′+ B′C′D′+ C′D′E′+ D′E′A′＝540

（1）填空：甲乙两位同学将　　　　转化为　　　，验证了　　　　。

（2）假如将上述五边形换成n边形，请你分别依据甲、乙两位同学的思路方法验证n边形内角和公式。