在△ABC中，AD是角平分线，AE是高线
①如图1所示，∠ABC=40°，∠ACB=70°，求∠DAE．
②如图2所示，∠ABC=30°，∠ACB=110°，求∠DAE．
③根据①、②两题的计算结果，请猜想∠DAE与∠ABC和∠ACB之间的关系．（用等式表示出来）

在△ABC中，AD是角平分线，AE是高线
①如图1所示，∠ABC=40°，∠ACB=70°，求∠DAE．
②如图2所示，∠ABC=30°，∠ACB=110°，求∠DAE．
③根据①、②两题的计算结果，请猜想∠DAE与∠ABC和∠ACB之间的关系．（用等式表示出来）

已知：△ABC中，∠C＞∠B，AE平分∠BAC．
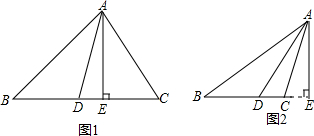
（1）如图①AD⊥BC于D，若∠C=70°，∠B=30°，请你用量角器直接量出∠DAE的度数；
（2）若△ABC中，∠B=α，∠C=β（α＜β），根据第一问的结果大胆猜想∠DAE与α、β间的等量关系，不必说理由；
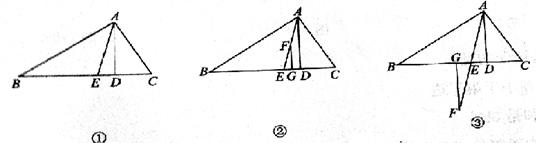
（3）如图②所示，在△ABC中AD⊥BC，AE平分∠BAC，F是AE上的任意一点，过F作FG⊥BC于G，且∠B=40°，∠C=80°，请你运用（2）中结论求出∠EFG的度数；
（4）在（3）的条件下，若F点在AE的延长线上（如图③），其他条件不变，则∠EFG的度数大小发生改变吗？说明理由．

如图①，在△ABC中，CD、CE分别是△ABC的高和角平分线，∠BAC=α，∠B=β（α＞β）．
（1）若α=70°，β=40°，求∠DCE的度数；
（2）试用α、β的代数式表示∠DCE的度数（直接写出结果）；
（3）如图②，若CE是△ABC外角∠ACF的平分线，交BA延长线于点E，且α-β=30°，求∠DCE的度数．