
题目列表(包括答案和解析)
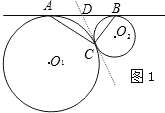
阅读下列材料:如图,⊙O1和⊙O2外切于点C,AB是⊙O1和⊙O2的外公切线,A、B为切点,求证:AC⊥BC.
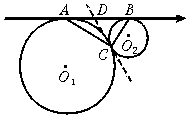
证实:过点C作⊙O1和⊙O2的内公切线交AB于D.
∵ DA、DC是⊙O1的切线,∴ DA=DC.
∴ ∠DAC=∠DCA.同理∠DCB=∠DBC.
又∵ ∠DAC+∠DCA+∠DCB+∠DBC=180°,∴ ∠DCA+∠DCB=90°.
即AC⊥BC.
根据上述材料,解答下列问题:
(1)在以上的证实过程中使用了哪些定理?请写出两个定理的名称或内容;
(2)以AB所在直线为x轴,过点C且垂直于AB的直线为y轴建立直角坐标系(如图11).已知A、B两点的坐标为(-4,0)、(1,0),求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式;
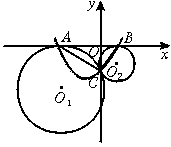
(3)根据(2)中所确定的抛物线,试判定这条抛物线的顶点是否落在两圆的连心O1O2上,并说明理由.
已知:在四边形ABCD中,AB=DC,AC=DB,AD≠BC。求证:四边形ABCD是等腰梯形。
下面是某同学证明这道题的过程:
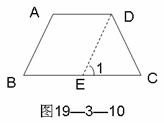
证明:过D作DE∥AB,交BC于E,如图19-3-10所示,则∠ABC=∠1。①
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB,②
∴∠ABC=∠DCB,③
∴∠1=∠DCB,④
∴AB=DC=DE,⑤
∴四边形ABED是平行四边形,⑥
∴AD∥BC,⑦
BE=AD,⑧
又∵AD≠BC,∴BE≠B,
∴点E,C是不同的点,DC不平行于AB。⑨
∵AB=DC,
∴四边形ABCD是等腰梯形。⑩
阅读后填空:
(1)上面的证明过程是否有错误?如有,错在第几步?答:_________;
(2)作DE∥AB的目的是__________;
(3)有人认为第⑨步是多余的,你认为它是否多余?为什么?_________;
(4)判断四边形ABED是平行四边形的依据为___________;
(5)判断四这形ABCD是等腰梯形的依据为_____________;
(6)若题设中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?为什么?
答:_________________。
如图所示,已知:四边形ABCD中,AB=DC、AC=BD、AD≠BC,求证:四边形ABCD是等腰梯形。

证明:过点D作DE∥AB,交BC于E,则∠ABE=∠1。 ①
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB. ②
∴∠ABC=∠DCB. ③
∴∠1=∠DCB. ④
∴AB=DC=DE。 ⑤
∴四边形ABED是平行四边形。 ⑥
∴AD∥BC, ⑦
BE=AD. ⑧
又∵AD≠BC,∴BE≠BC.
∴点E、C是不同的点,DC不平行AB. ⑨
又∵AB=CD,∴四边形ABCD是等腰梯形。 ⑩
读后完成下列各小题。
(1)证明过程是否有错误?如有错在第几步上。答:______________。
(2)作DE∥AB的目的是________________________。
(3)有人认为第9步是多余的,你的看法是______________。
(4)判断四边形ABED为平行四边形的依据是______________。
(5)判断四边形ABCD是等腰梯形的依据是______________。
(6)若题设中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?你的意见是______________。
阅读:下面是某同学证明一道几何题的过程.
已知:四边形ABCD中,AB=DC,AC=BD,AD≠BC
求证:四边形ABCD是等腰梯形.
证明:过D作DE∥AB交BC于E(如图所示),
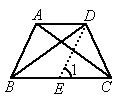
则∠ABE=∠1,①
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB,②
∴∠ABC=∠DCB,③
∴∠1=∠DCB,④
∴AB=DC=DE,⑤
∴四边形ABED是平行四边形.⑥
∴AD∥BC.⑦
BE=AD.⑧
又AD≠BC,∴BE≠BC.
∴点E,C是不同的点,DC不平行于AB.⑨
∵AB=CD,∴四边形ABCD是等腰梯形.⑩
读后填空:
(1)证明过程是否有错误?如有,错在第几步.答:__________;
(2)作DE∥AB的目的是__________;
(3)有人认为第9步是多余的,你认为是否多余?为什么?答:________;
(4)判断四边形ABED为平行四边形的依据是__________;
(5)判断四边形ABCD是等腰梯形的依据是__________;
(6)若题目中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?为什么?答_________.
 阅读下列材料:
阅读下列材料: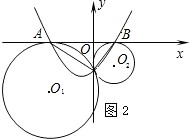
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com