
题目列表(包括答案和解析)
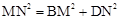 ,请证明这个等量关系;
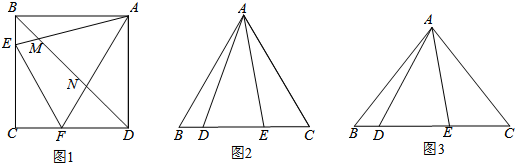
,请证明这个等量关系;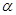 ,(0°<
,(0°<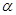 <90°),∠DAE=
<90°),∠DAE=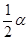 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: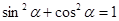 】
】
将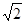 ,
,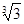 ,
,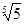 用不等号连接起来为( )
用不等号连接起来为( )
A. 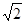 <
<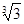 <
<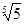 B.
B.
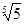 <
<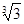 <
<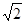
C. 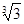 <
<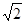 <
<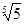 D.
D.
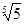 <
<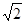 <
<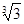
阅读下面的文字,解答问题.
大家知道 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1< <2,所以
<2,所以 的整数部分为1,将
的整数部分为1,将 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分 -1,根据以上的内容,解答下面的问题:
-1,根据以上的内容,解答下面的问题:
(1) 的整数部分是_______,小数部分是______;
的整数部分是_______,小数部分是______;
(2)1+ 的整数部分是_______,小数部分是____;
的整数部分是_______,小数部分是____;
(3)若设2+ 的整数部分是x,小数部分是y,求x-
的整数部分是x,小数部分是y,求x- y的值
y的值
把两个全等的直角三角板ABC和EFG叠放在一起,且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF的长均为4。
(1)当EG⊥AC于点K,GF⊥BC于点H时,如图23-1,求GH:GK的值.
(2)现将三角板EFG由图23-1所示的位置绕O点沿逆时针方向旋转,旋转 角满足条件:
角满足条件:
0°< <30°,如图23-2,EG交AC于点K,GF交BC于点H,GH:GK的值是否改变?证明你的结论.
<30°,如图23-2,EG交AC于点K,GF交BC于点H,GH:GK的值是否改变?证明你的结论.


(本小题满分12分)
已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在![]() 轴上.
轴上.

1.(1)求m的值及这个二次函数的解析式;
2.(2)若P(![]() ,0) 是
,0) 是![]() 轴上的一个动点,过P作
轴上的一个动点,过P作![]() 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<![]() < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,
问是否存在一点P,使以M、N、D、E
为顶点的四边形是平行四边形?若存在,
请求出此时P点的坐标;若不存在,请
说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com