练习册

  • 练习册
  • 试题
    1． 填空: (1)-235的底数为 .指数为 , 2= , -42= , 3= , -3×23= , (-3)3= , -(-2)5= ; (-)4= , (-)3= ; (-1)2004= , 02003= . (3) 的平方为. 的立方为216. 若a2=25,则a= .若a3= -27.则a= . 2+︱b+4︱=0.则a= ,b= ,a-b= (5)一个有理数的三次幂是负数.则这个数的四次幂是 数, (6)有理数的二次幂与它的三次幂相等.则a的值为 , 【查看更多】

     

    题目列表(包括答案和解析)

    下面的说法中，正确的个数是(　　)．

    ①长方体是四棱柱　　②四棱柱的底面是四边形　　③长方体的每个侧面只能都是长方形，不能含有正方形　　④正方体的每个面都是正方体　　⑤过某顶点的三条棱长相等的长方体是正方体　　⑥正方体是棱柱．

    [　　]

    A．2个

    B．3个

    C．4个

    D．5个

    查看答案和解析>>

    下面说法正确的有

    ①圆柱体的上、下两个圆一样大　　②圆柱、圆锥的底面都是圆　　③圆柱是由两个面围成的　　④长方体的面不可能是正方形

    [　　]

    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    如图，这些等腰三角形与正三角形的形状有差异，我们把它与正三角形的接近程度称为“正度”．在研究“正度”时，应保证相似三角形的“正度”相等．

    　　设等腰三角形的底和腰分别为a、b，底角和顶角分别为α、β，要求“正度”的值是非负数．

    　　同学甲认为：可用式子|a－b|来表示“正度”，|a－b|的值越小，表示的等腰三角形越接近正三角形；

    　　同学乙认为：可用式子|α－β|来表示“正度”，|α－β|的值越小，表示的等腰三角形越接近正三角形．

    探究：(1)他们的方案哪个较为合理，为什么？

    (2)对你认为不够合理的方案，请加以改进(给出式子即可)；

    (3)请再给出一种衡量“正度”的表达式．

    查看答案和解析>>

    　　(安徽省2003年中考试题)如图，这些等腰三角形与正三角形的形状有差异，我们把它与正三角形的接近程度称为“正度”．在研究“正度”时，应保证相似三角形的“正度”相等．

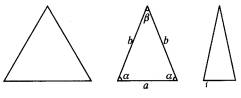
    　　设等腰三角形的底和腰分别为a、b，底角和顶角分别为、β．要求“正度”的值是非负数．

    　　同学甲认为：可用式子|a-b|来表示“正度”，|a-b|值越小，表示等腰三角形越接近正三角形．

    　　同学乙认为：可用式子|α-β|来表示“正度”，|α-β|的值越小，表示等腰三角形越接近正三角形．

    　　探究：(1)他们的方案哪个较合理，为什么？

    　　(2)对你认为不够合理的方案，请加以改进(给出式子即可)；

    　　(3)请再给出一种衡量“正度”的表达式．

     

    查看答案和解析>>

    在一次测验中的解答的填空题如下：
    （1）当m取1时，一次函数y=（m-2）x+3，y随x的增大而增大；
    （2）等腰梯形ABCD，上底AD=2，下底BE=8，∠B=60°，则腰长AB=6；　
    （3）菱形的边长为6cm，一组相邻角的比为l：2，则菱形的两条对角线的长分别为6cm和6数学公式cm；　
    （4）如果一个多边形的内角和比它的外角和的3倍少180°，则这个多边形是五边形．　
    你认为正确的填空个数是


    1. A.
      1个
    2. B.
      2个
    3. C.
      3个
    4. D.
      4个

    查看答案和解析>>


    同步练习册答案