
题目列表(包括答案和解析)
(1)设一长方体盒子高为10 cm,底面是正方形,这个长方体的体积V(cm3)与底面边长a(cm)的关系式为V=10a2;
(2)某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元,出租车车费y(元)与行程x(千米)之间的函数关系式为y=1.6(x-2)+7(x≥2);
(3)计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的关系为n=![]() ;
;
(4)用总长为60 m的篱笆围成矩形场地,矩形面积S(m2)与一边长l(m)之间的关系式为S=l(60-l).
指出下列各关系中的变量和常量:
①周长C与半径r的关系式是 ;
;
常量是_________,变量是_________;
②多边形的内角和A与边数n之间的关系式是A=(n-2)×180°;
常量是_________,变量是_________;
③底边为定值a的三角形面积与底边上的高h之间的关系式为 .
.
常量是_________,变量是_________.
如图(1),某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线形水流在与喷头底部A的距离为1 m处达到距地面最大高度2.25 m,试在恰当的直角坐标系中求出与该抛物线水流对应的二次函数关系式

学生小龙在解答图(1)所示的问题时,具体解答如下:
①以水流的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴,建立如图(2)所示的平面直角坐标系;
②设抛物线水流对应的二次函数关系式为y=ax2;
③根据题意可得B点与x轴的距离为1 m,故B点的坐标为(-1,1);
④代入y=ax2得-1=a·1,所以a=-1;
⑤所以抛物线水流对应的二次函数关系式为y=-x2
数学老师看了小龙的解题过程说:“小龙的解答是错误的”
(1)请指出小龙的解答从第________步开始出现错误,错误的原因是什么?
(2)请你写出完整的正确解答过程
某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图1,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
(1
)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积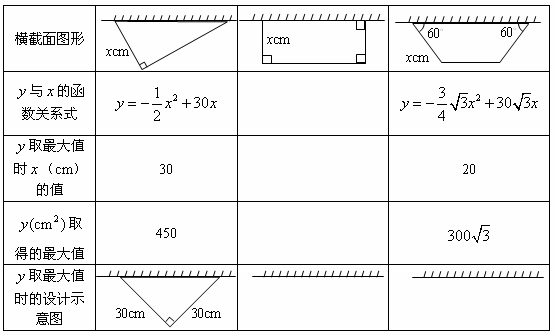
(2
)在研究性学习小组展示研究成果时,小华同学指出:图2中摰捉俏-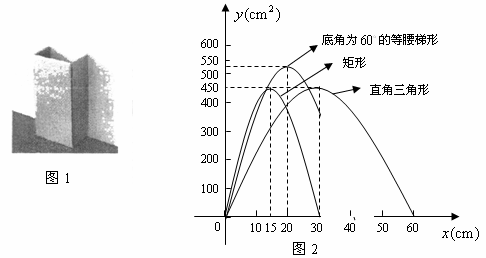
| |||||||||||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com