
题目列表(包括答案和解析)
| 1 |
| 5 |
| 11 |
| 5 |
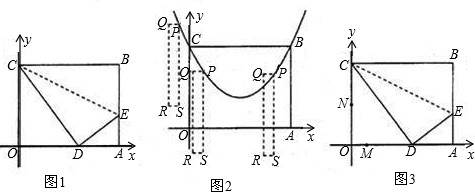
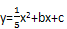 过点C、B.
过点C、B. 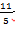 个单位,当矩形PQRS在滑动过程中被x轴分成上下两部分的面积比为2:3时,求点P的坐标;
个单位,当矩形PQRS在滑动过程中被x轴分成上下两部分的面积比为2:3时,求点P的坐标; 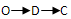 的路线运动,点N以每秒8个单位长度的速度沿折线OCD按
的路线运动,点N以每秒8个单位长度的速度沿折线OCD按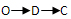 的路线运动,当M、N两点相遇时,它们都停止运动.设M、N同时从点O出发t秒时,△OMN的面积S.①求出S与t的函数关系式,并写出t的取值范围:②设S0是①中函数S的最大值,那么S0= ________
的路线运动,当M、N两点相遇时,它们都停止运动.设M、N同时从点O出发t秒时,△OMN的面积S.①求出S与t的函数关系式,并写出t的取值范围:②设S0是①中函数S的最大值,那么S0= ________ 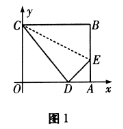
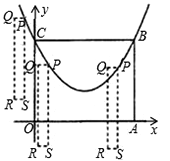
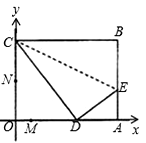
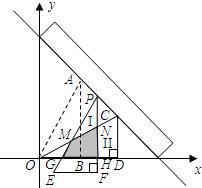 从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.
从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设 与
与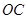 分别交于点
分别交于点 ,与
,与 轴分别交于点
轴分别交于点 .
.
(1)求直线 所对应的函数关系式;
所对应的函数关系式;
(2)当点 是线段
是线段 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点 到
到 轴的距离
轴的距离 与线段
与线段 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com