
题目列表(包括答案和解析)
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
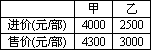
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后获毛利润共2.1万元(毛利润=(售价-进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量,已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第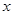 天(
天(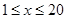 且
且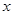 为整数)的捕捞与销售的相关信息如表:
为整数)的捕捞与销售的相关信息如表:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-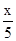 |
| 捕捞量(kg) | 950-10x |
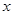 天的收入
天的收入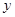 (元)与
(元)与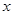 (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)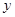 随
随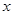 的变化情况,并指出在第几天
的变化情况,并指出在第几天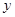 取得最大值,最大值是多少?
取得最大值,最大值是多少?春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第 天(
天(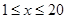 且
且 为整数)的捕捞与销售的相关信息如表:
为整数)的捕捞与销售的相关信息如表:
|
鲜鱼销售单价(元/kg) |
20 |
|
单位捕捞成本(元/kg) |
5- |
|
捕捞量(kg) |
950-10x |
(1)在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的 (填“增加”或“减少”了多少kg.)
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第 天的收入
天的收入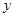 (元)与
(元)与 (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(3)试说明⑵中的函数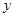 随
随 的变化情况,并指出在第几天
的变化情况,并指出在第几天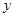 取得最大值,最大值是多少?
取得最大值,最大值是多少?
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下表:
为整数)的捕捞与销售的相关信息如下表:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5- |
| 捕捞量(kg) | 950-10x |
⑴ 在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的 (填“增加”或“减少”了多少kg.)
⑵ 假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(3) 试说明⑵中的函数![]() 随
随![]() 的变化情况,并指出在第几天
的变化情况,并指出在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下表:
为整数)的捕捞与销售的相关信息如下表:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5- |
| 捕捞量(kg) | 950-10x |
⑴ 在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的 (填“增加”或“减少”了多少kg.)
⑵ 假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(3) 试说明⑵中的函数![]() 随
随![]() 的变化情况,并指出在第几天
的变化情况,并指出在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com