如图，抛物线与x轴交于A(x₁,0)，B(x₂,0)两点，且x₁＞x₂，与y轴交于点C(0,4)，其中x₁,x₂是方程x²-2x-8=0的两个根.

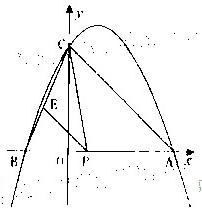
 (1)求这条抛物线的解析式；

　　(2)点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；

　　(3)探究：若点Q是抛物线对称轴上的点，是否存在这样的点Q，使△QBC成为等腰三角形，若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由.

如图，抛物线与x轴交于A(x₁,0)，B(x₂,0)两点，且x₁＞x₂，与y轴交于点C(0,4)，其中x₁,x₂是方程x²-2x-8=0的两个根.

 (1)求这条抛物线的解析式；

　　(2)点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；

　　(3)探究：若点Q是抛物线对称轴上的点，是否存在这样的点Q，使△QBC成为等腰三角形，若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由.

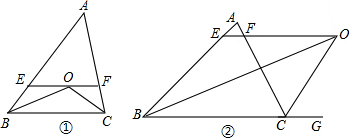如图①，△ABC中，∠ABC、∠ACB的平分线交于O点，过O点作BC平行线交AB、AC于E、F． 试说明：EO=BE　
探究一：请写出图①中线段EF与BE、CF间的关系，并说明理由．
探究二：如图②，△ABC若∠ABC的平分线与△ABC的外角平分线交于O，过点O作BC的平行线交AB于E，交AC于F．这时EF与BE、CF的关系又如何？请直接写出关系式，不需要说明理由．

问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA。

　 探究∠DBC与∠ABC度数的比值。你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明。

　 (1) 当∠BAC=90°时，依问题中的条件补全右图。 观察图形，AB与AC的数量关系为　　 当推出∠DAC=15°时，可进一步推出∠DBC的度数为　　 ；可得到?DBC与∠ABC度数的比值为　　 ；

　 (2) 当∠BAC＝90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与(1)中的结论相同，写出你的猜想并加以证明。

问题背景

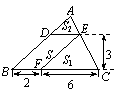
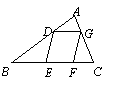
（1）如图22（1），△ABC中，DE∥BC分别交AB，AC于D，E两点，

过点E作EF∥AB交BC于点F．请按图示数据填空：

四边形DBFE的面积      ，△EFC的面积      ，

△ADE的面积      ．　　　　　　　　 　　　　 　　　　　  

探究发现

（2）在（1）中，若，，DE与BC间的距离为．请证明．拓展迁移

（3）如图22（2），□DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为2、5、3，试利用

（2）中的结论求△ABC的面积．　　　　　　　　　　　　　　　  

（1）                         （2）