
题目列表(包括答案和解析)
明天要开运动会了,小明很想有一双新运动鞋,爸爸说只要小明能算出自己穿多少码的鞋子便买给他.小明想了想,拿出妈妈36码的鞋子量得长23cm,拿出爸爸41码的鞋子量得长25.5cm,那么自己21.5cm的鞋子是多少码呢?经过一阵思索,小明终于想到了算法,并很快地算出了自己要穿的码数.为了检验自己设计的算法是否正确,小明跑到隔壁小刚哥哥家,了解到小刚哥哥38码的鞋子长24cm,正好符合自己的计算方法.你能说出小明是如何解决这个问题的吗?请给出算法,并检验其正确性.
数学老师在黑板上出这样的一道题:
![]()
| |||||||||||||||
古希腊的毕达哥拉斯学派主张“万物皆数”,他们试图用数学方法来解释世界,他们把一些正整数分别排成三角形、正方形等,称为三角形数,正方形数,……例如,三角形数:
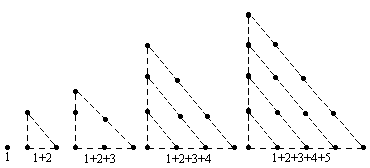
试写出第n个三角形数Sn与n的关系式.
(1)根据Sn的关系式,算一算著名数学家高斯小时候做过的算术题1+2+3+…+100=?
(2)根据Sn的公式,说明平面上n+1个不同的点可以连成多少条线段.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com