
题目列表(包括答案和解析)
形如:
3+ 的分数,分数里有分数,一个接着一个,可称之为连分数.
的分数,分数里有分数,一个接着一个,可称之为连分数.
连分数可以化成普通分数,例如:
3+ =3+
=3+![]() =3+
=3+![]() =3+
=3+![]() .
.![]() 是我国数学家祖冲之所作的密率.而3+
是我国数学家祖冲之所作的密率.而3+![]() 称为疏率,是何承天(370~447年)最先采用的.它们都可以作为圆周率π的近似值.实际上,π=3.14159265…,
称为疏率,是何承天(370~447年)最先采用的.它们都可以作为圆周率π的近似值.实际上,π=3.14159265…,![]() =3.14159292…,
=3.14159292…,![]() =3.14285714….
=3.14285714….
20世纪60年代,我国著名数学家华罗庚先生专门写了一本小册子《从祖冲之的圆周率谈起》,向数学爱好者介绍连分数的理论与应用,其中就包括了连分数与圆周率的关系.
想一想:你会把下列连分数化为普通分数吗?1+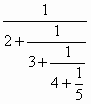
| 355 |
| 113 |
| 22 |
| 7 |
| 355 |
| 113 |
| 22 |
| 7 |
A、
| ||||
B、
| ||||
C、π<
| ||||
D、
|
| 355 |
| 113 |
| 22 |
| 7 |
| 355 |
| 113 |
| 22 |
| 7 |
A.
| B.
| ||||||||
C.π<
| D.
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com