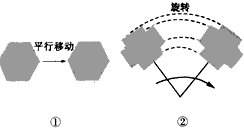
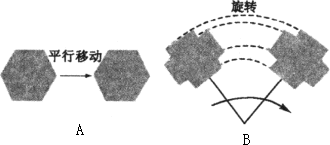
我们知道，对于两个图形，如果沿一条直线对折后，它们能完全重合，那么这两个图形成轴对称．既然成轴对称的两个图形能够完全重合，那么“关于某条直线对称的两个图形是全等形”．通常把图形从一种情况到另一种情况的对应关系称作图形变换，对称就是一种变换．观察图A、B容易看出，经过图形变换后，变换前后图形的位置改变了，但它的形状和大小并没有改变，这种只改变图形的位置，而不改变其形状、大小的图形变换叫做全等变换．前面说到的对称变换是一种全等变换；图A、B所示的变换分别是平移变换和旋转变换，它们都是全等变换(如图所示)．

请你回答：全等变换的两个图形面积相等吗？为什么？

操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．

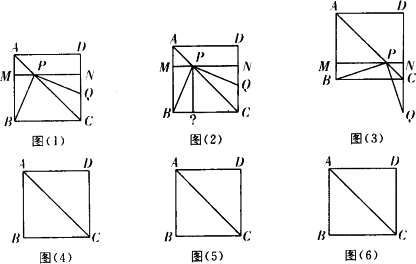
探究：设A、P两点间的距离为x．

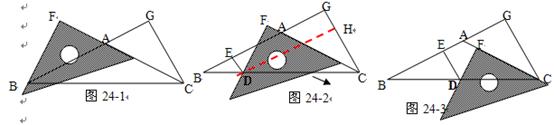
⑴当点Q在CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到的结论(如图⑴)．

⑵当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域(如图⑵)．

⑶当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由(如图⑶)．(图⑷、图⑸、图⑹的的形状、大小相同，图⑷供操作、实验用，图⑸和图⑹备用)

在△ABC中，AB＝AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．

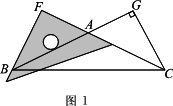
(1)在图1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；

(2)当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE＋DF与CG之间满足的数量关系，然后证明你的猜想；

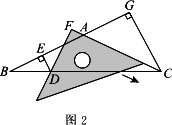
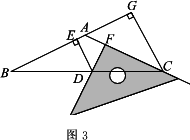
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上，且点F与点C不重合)时，(2)中的猜想是否仍然成立？(不用说明理由)