
题目列表(包括答案和解析)
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.
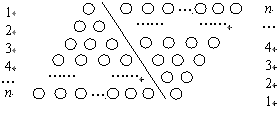
(1)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)
(2)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.
数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整数.
对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.
如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.

(1)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
(2)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)
已知:关于
x的一元二次方程mx2-(2m+n)x+m+n=0 ①.(1)求证:方程①有两个实数根;
(2)求证:方程①有两个实数根;
(3)设方程①的另一个根为x1,若m+n=2,m为正整数且方程①有两个不相等的整数根时,确定关于x的二次函数y=mx2-(2m+n)x+m+n的解析式;
(4)在(3)的条件下,把Rt△ABC放在坐标系内,其中∠CAB=90°,点A、B的坐标分别为(1,0)、(4,0),BC=5,将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离.
如图,将矩形OABC放置在平面直角坐标系中,点D在边OC上,点E在边OA上,把矩形沿直线DE翻折,使点O落在边AB上的点F处,且tan∠BFD=![]() .若线段OA的长是一元二次方程x2-7x-8=0的一个根,又2AB=3OA.请解答下列问题:
.若线段OA的长是一元二次方程x2-7x-8=0的一个根,又2AB=3OA.请解答下列问题:
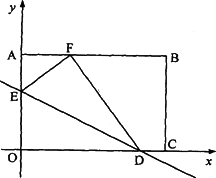
(1)求点B、F的坐标:
(2)求直线ED的解析式:
(3)在直线ED、FD上是否存在点M、N,使以点C、D、M、N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
传说波斯国王,出了下列算题悬赏大臣:
我的3只金碗里放着数目相同的珍珠,我把第一只金碗里的珍珠的一半给我大儿子,把第二只金碗里的珍珠的 给我二儿子,把第三只金碗里的
给我二儿子,把第三只金碗里的 珍珠的给我的小儿子,然后再把第一只金碗里的4颗珍珠给我大女儿,把第二只金碗里的6颗珍珠给我二女儿,把第三只金碗里的2颗珍珠给我小女儿,这样第一只金碗里剩下38颗珍珠,第二只金碗里剩下22颗珍珠,第三只金碗里剩下19颗珍珠,试问:我的3只金碗里原来分别放着多少颗珍珠?
珍珠的给我的小儿子,然后再把第一只金碗里的4颗珍珠给我大女儿,把第二只金碗里的6颗珍珠给我二女儿,把第三只金碗里的2颗珍珠给我小女儿,这样第一只金碗里剩下38颗珍珠,第二只金碗里剩下22颗珍珠,第三只金碗里剩下19颗珍珠,试问:我的3只金碗里原来分别放着多少颗珍珠?
第一个大臣认为第一只金碗里的一半为(38+4)颗,所以第一只金碗里有2(38+4)=84(颗).第二只金碗里的 为(22+6)颗,所以第二只金碗里有3(22+6)=84(颗).第三只金碗里的
为(22+6)颗,所以第二只金碗里有3(22+6)=84(颗).第三只金碗里的 为(19+2)颗,所以第三只金碗里有4(19+2)=84(颗).所以国王三只金碗里分别放着84颗珍珠.
为(19+2)颗,所以第三只金碗里有4(19+2)=84(颗).所以国王三只金碗里分别放着84颗珍珠.
第二个大臣设第一只金碗里有x颗珍珠,由题意列出方程 x+4+38=x解得x=84,设第二只金碗里有y颗珍珠,由题意列出方程专
x+4+38=x解得x=84,设第二只金碗里有y颗珍珠,由题意列出方程专 y+6+22=y,解得y=84,设第三只金碗里有z颗珍珠,由题意列出方程
y+6+22=y,解得y=84,设第三只金碗里有z颗珍珠,由题意列出方程 z+2+19=z,解得z=84.所以国王三只金碗里分别放着84颗珍珠
z+2+19=z,解得z=84.所以国王三只金碗里分别放着84颗珍珠
第三个大臣设国王的每只金碗里放着x颗珍珠,a代表国王给儿子的珍珠占碗里的珍珠数的几分之几,b代表国王给女儿的珍珠数,c代表碗里剩下的珍珠数.由题意列出方程ax+b+c=x,(1-a)x=b+c,x= .
.
请你将(1)b=4,c=38,a= ;(2)b=6,c=22,a=
;(2)b=6,c=22,a= ;(3)b=2,c=19,a=
;(3)b=2,c=19,a= 分别代入x=
分别代入x= ,计算一下x的值是否与第一个、第二个大臣算出的珍珠数相符?并请你为波斯国王当一回“参谋”,三个大臣该如何得到国王的悬赏?
,计算一下x的值是否与第一个、第二个大臣算出的珍珠数相符?并请你为波斯国王当一回“参谋”,三个大臣该如何得到国王的悬赏?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com