甲每小时走a千米，乙每小时走b千米(a＞b)，若两人同时同地出发．

(1)反向行走x小时后，两人相距__________千米；

(2)同向行走y小时后，两人相距__________千米；

(3)他们从A地出发到达相距x千米的B地．若甲比乙早到2小时，则题中的一个等量关系是__________千米．

甲每小时走a千米，乙每小时走b千米(a>b)，若两人同时同地出发.

①反向行走x小时后，两人相距_______千米；

②同向行走y小时后，两人相距_______千米；

③他们从A地出发到达相距x千米的B地.若甲比乙早到2小时，则题中的一个等量关系是_______.

 

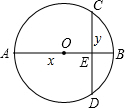善于归纳和总结的小明发现，“数形结合”是初中数学的基本思想方法，被广泛地应用在数学学习和解决问题中．用数量关系描述图形性质和用图形描述数量关系，往往会有新的发现．小明在研究垂直于直径的弦的性质过程中（如图，直径AB⊥弦CD于E），设AE=x，BE=y，他用含x，y的式子表示图中的弦CD的长度，通过比较运动的弦CD和与之垂直的直径AB的大小关系，发现了一个关于正数x，y的不等式，你也能发现这个不等式吗？写出你发现的不等式．