如图，AB为⊙O的直径，AM和BN是它的两条切线，E为⊙O的半圆弧上一动点（不与A、B重合），过点E的直线分别交射线AM、BN于D、C两点，且CB＝CE．

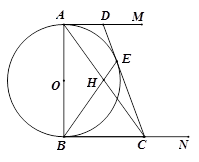
1.求证：CD为⊙O的切线

2.若tan∠BAC＝，求 的值

如图，在下列矩形ABCD中，已知：AB＝a，BC＝b（a＜b），假定顶点在矩形边上的菱形叫做矩形的内接菱形，现给出（Ⅰ）、（Ⅱ）、（Ⅲ）三个命题：

命题（Ⅰ）：图①中，若AH＝BG＝AB，则四边形ABGH是矩形ABCD的内接菱形；

命题（Ⅱ）：图②中，若点E、F、G和H分别是AB、BC、CD和DE的中点，则四边形EFGH是矩形ABCD的内接菱形；

命题（Ⅲ）：图③中，若EF垂直平分对角线AC，变BC于点E，交AD于点F，交AC于点O，则四边形AECF是矩形ABCD的内接菱形.

请解决下列问题：

1.命题（Ⅰ）、（Ⅱ）、（Ⅲ）都是真命题吗？请你在其中选择一个，并证明它是真命题或假命题；

2.画出一个新的矩形内接菱形（即与你在（1）中所确认的，但不全等的内接菱形）.

3.试探究比较图①，②，③中的四边形ABGH、EFGH、AECF的面积大小关系

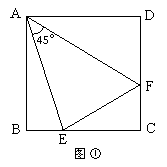
如图①，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45 °

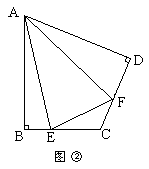
，则有结论EF＝BE＋FD成立；                                                                                                  1.如图②，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是BC、CD上的点，且∠EAF是∠BAD的一半，那么结论EF＝BE＋FD是否仍然成立？若成立，请证明；若不成立，请说明理由；

2.若将（1）中的条件改为：在四边形ABCD中，AB＝AD，∠B+∠D＝180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF＝BE＋FD是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.

如图，在矩形ABCD中，有一个菱形BFDE（点E、F分别在线段AB、CD上），记它们的面积分别为和. 现给出下列命题：

①若，则；②若，则DF＝2AD.

那么，下面判断正确的是（   ）

A．①是真命题，②是真命题             B．①是真命题，②是假命题

C．①是假命题，②是真命题          D．①假真命题，②假真命题