
题目列表(包括答案和解析)

图7-2-27
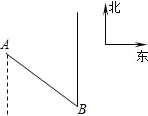 据气象台预报,有一由南向北移动的台风,其中心在南偏东45°,离我市A400km的B地登陆(如图所示).已知在台风中心260km的范围内的地方都会受到台风侵袭,那么我市会不会受到此次台风的侵袭?为什么?
据气象台预报,有一由南向北移动的台风,其中心在南偏东45°,离我市A400km的B地登陆(如图所示).已知在台风中心260km的范围内的地方都会受到台风侵袭,那么我市会不会受到此次台风的侵袭?为什么?| 3 |
| 2 |


 4、如图,△ABC≌△ADE,已知在△ABC中,AB边最长,BC边最短,则△ADE中三边的大小关系是( )
4、如图,△ABC≌△ADE,已知在△ABC中,AB边最长,BC边最短,则△ADE中三边的大小关系是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com