
题目列表(包括答案和解析)
|
| A、用加减法 |
| B、用代入法 |
| C、先用①-②,再用代入法 |
| D、先用①+②,再用代入法 |
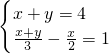
 -
- =1
=1 -
- =1,
=1, =
= -1,
-1, =
=

 代入③得y=4-
代入③得y=4- =3
=3
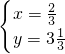 .
. ,y=3
,y=3 代入①得,左边=x+y=
代入①得,左边=x+y= +3
+3 =4,右边=4.
=4,右边=4. ,y=3
,y=3 代入②得
代入②得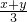 -
- =
=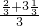 -
-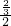 =
= -
- =1,右边=1.
=1,右边=1.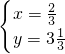 是原方程组的解.
是原方程组的解.
|
| x+4-x |
| 3 |
| x |
| 2 |
| 4 |
| 3 |
| x |
| 2 |
| x |
| 2 |
| 4 |
| 3 |
| x |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
|
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| x+y |
| 3 |
| x |
| 2 |
| ||||
| 3 |
| ||
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
|
列方程(组)解应用题:
一辆公共汽车上午8∶00以每小时40千米的速度从A站驶往B站.上午10∶00,一辆小汽车又从A站出发驶往B站,结果小汽车比公共汽车早40分钟到达B站.已知两车的速度之比为1∶3,问A、B两站相距多少千米?公共汽车是什么时候到达B站的?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com