
题目列表(包括答案和解析)
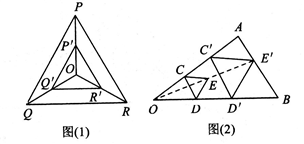
如果一个多边形的每个外角均相等,并且它的内角和等于![]() ,那么它的每个内角都等于________度.
,那么它的每个内角都等于________度.
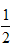 、点P
、点P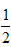 、点O
、点O个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做
位似中心。利用三角形的位似可以将一个三角形缩小或放大。
(1)选择:如图(1),点O是等边△PQR的中心,P’Q’R’分别是OP、OQ、OR的
中点,则△P’Q’R’与是△PQR是位似三角形,此时,△P’Q’R’与△PQR的位似比,位
似中心分别为 ( )
A. 2,点P B. ,点P C. 2,点O D. ,点O
(2)如图(2),用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应的
问题。画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②
连结OE并延长,交AB于点E’,过点E’作E’C’//EC,交OA于点C’,作E’D’//ED,
交OB于点D’;③连结C’D’,则△C’D’E’ 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com