
题目列表(包括答案和解析)
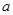 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为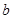 的小正方形(
的小正方形(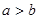 ),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于
),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于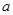 ,
,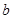 的恒等式为( ).
的恒等式为( ).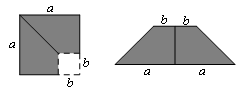
A. | B. |
C.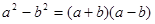 | D.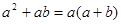 |
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)


请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.

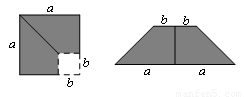
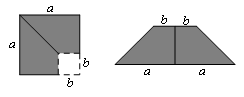
如下图,在边长为 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为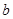 的小正方形(
的小正方形(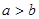 ),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于
),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于 ,
,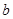 的恒等式为( ).
的恒等式为( ).
A.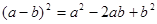 B.
B.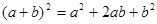
C. D.
D.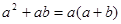
如图,在边长为 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为 的小正方形(
的小正方形( >
> ),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于
),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于 、
、 的恒等式为( )
的恒等式为( )
A. |
B.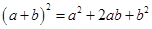 |
C. |
D. |
如下图,在边长为![]() 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为![]() 的小正方形(
的小正方形(![]() ),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于
),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于![]() ,
,![]() 的恒等式为( ).
的恒等式为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com