（1）解二元一次方程组：

3x-y=-4① x-2y=-3②

（2）试运用解二元一次方程组的思想方法，解三元一次方程组：

x+y+z=22① 3x+y=47② x-4z=2③

．

在学习因式分解时，我们学习了提公因式法和公式法（平方差公式和完全平方公式），事实上，除了这两种方法外，还有其它方法可以用来因式分解，比如配方法．例如，如果要因式分解x²+2x-3时，显然既无法用提公因式法，也无法用公式法，怎么办呢？这时，我们可以采用下面的办法：
x²+2x-3=x²+2×x×1+1²-1-3------①
=（x+1）²-2²------②
=…
解决下列问题：
（1）填空：在上述材料中，运用了的思想方法，使得原题变为可以继续用平方差公式因式分解，这种方法就是配方法；
（2）显然所给材料中因式分解并未结束，请依照材料因式分解x²+2x-3；
（3）请用上述方法因式分解x²-4x-5．

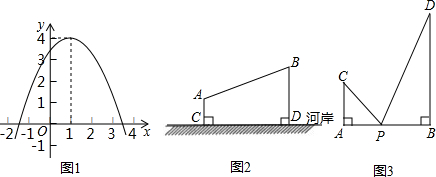
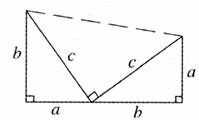
（2011•新华区一模）我们知道：根据二次函数的图象，可以直接确定二次函数的最大（小）值；根据“两点之间，线段最短”，并运用轴对称的性质，可以在一条直线上找到一点，使得此点到这条直线同侧两定点之间的距离之和最短．
这种数形结合的思想方法，非常有利于解决一些数学和实际问题中的最大（小）值问题．请你尝试解决一下问题：
（1）在图1中，抛物线所对应的二次函数的最大值是；
（2）在图2中，相距3km的A、B两镇位于河岸（近似看做直线l）的同侧，且到河岸的距离AC=1千米，BD=2千米，现要在岸边建一座水塔，分别直接给两镇送水，为使所用水管的长度最短，请你：
①作图确定水塔的位置；
②求出所需水管的长度（结果用准确值表示）
（3）已知x+y=6，求

x2+9

+

y2+25

的最小值；
此问题可以通过数形结合的方法加以解决，具体步骤如下：
①如图3中，作线段AB=6，分别过点A、B，作CA⊥AB，DB⊥AB，使得CA=，DB=；
②在AB上取一点P，可设AP=，BP=；
③

x2+9

+

y2+25

的最小值即为线段和线段长度之和的最小值，最小值为．

（2012•白下区二模）（1）解方程组 

y=x+1 3x-2y=-1

（2）请运用解二元一次方程组的思想方法解方程组

x+y=1 x+y2=3

．